Home 数学 微分几何

微分形简单来说就是在积分

∫f(x)dx,∬f(x,y)dxdy\int f(x)dx,\quad \iint f(x,y)dxdy

中，形如

f(x)dx,f(x,y)dxdyf(x)dx, f(x,y)dxdy

的部分

微分形具有不同的次数，也可以定义在不同维度的空间中。为了方便理解，我们首先从二维空间的 11 次微分形开始导入

# 1 - 形式

令 U⊂R2U \subset \mathbb R^2 为开集
对于定点 p∈U\boldsymbol p \in U，令以 p\boldsymbol p 为起点的所有有向线段全体构成集合 TpUT_{\boldsymbol p}U，并将以 p\boldsymbol p 为起点，q\boldsymbol q 为终点的有向线段记为 pq→\overrightarrow{\boldsymbol{pq}}，则

TpU={pq→∣q∈U}T_{\boldsymbol p}U = \{\overrightarrow{\boldsymbol{pq}} | \boldsymbol q \in U\}

由于有向线段 pq→\overrightarrow{\boldsymbol{pq}} 和向量 q−p\boldsymbol{q}-\boldsymbol{p} 等价，所以 TpUT_{\boldsymbol p}U 实际上成为 R2\mathbb R^2 （的一个平移）

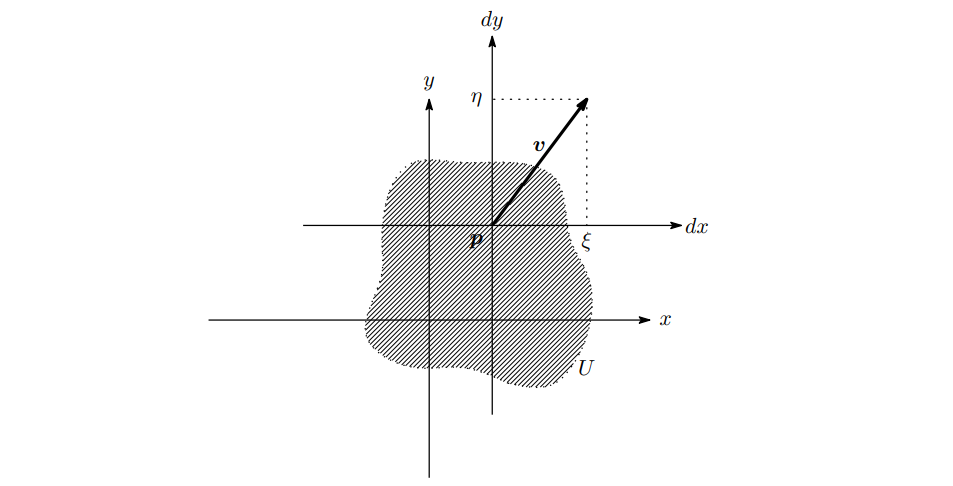
对于原平面 R2\mathbb R^2 上的坐标轴 x,yx,y，使新平面 TpUT_{\boldsymbol p}U 上的坐标轴为 dx,dydx,dy
则对于点 v=t(ξ,η)∈TpU\boldsymbol v = {}^t(\xi, \eta) \in T_{\boldsymbol p}U
其 dx,dydx, dy 坐标为 (ξ,η)(\xi, \eta)，如图
dxdy.png

同时，也可以将 dx,dydx, dy 视为坐标函数

dx:(ξη)↦ξ,dy:(ξη)↦ηdx: \begin{pmatrix} \xi \\ \eta \end{pmatrix} \mapsto \xi, \quad dy: \begin{pmatrix} \xi \\ \eta \end{pmatrix} \mapsto \eta

通过这样的空间处理，本质上实现了：将一个定点 p\boldsymbol p 的附近方法，让曲面近似为平面，使得非线性问题转变为线性问题
也就是微积分思想中的无限分割
那么此时

定义 R2\mathbb R^2 上的 1 - 形式
令 U⊂R2U \subset \mathbb R^2 为开集
f,gf, g 分别为 xyxy 平面上定义的两个 C∞C^\infty 函数

与 p∈U,v∈TpU\boldsymbol p \in U, \boldsymbol v \in T_{\boldsymbol p}U 对应的函数

fdx+gdy:TpU→Rfdx + gdy: T_{\boldsymbol p}U \to \mathbb R

v→f(p)dx(v)+g(p)dy(v)\boldsymbol v \to f(\boldsymbol p)dx(\boldsymbol v) + g(\boldsymbol p)dy(\boldsymbol v)

称为 U⊂R2U \subset \mathbb R^2 上的 C∞C^\infty 级 11 次微分形式
或者称为 1 - 形式 (1-form)「1 - 形式」

此处的 f,gf,g 本质上是向量函数的分量坐标
通过让各自的分量乘上 v\boldsymbol v 的分量，可以获取到：在变化 v\boldsymbol v 的过程中，函数 f,gf,g 的变化量
最后加起来得到一个向量函数的 “量纲”
通过对这个量纲进行累加（积分），也就得到了我们需要计算的总量
所以微分形的本质是：将非线性的变化转变为线性的微小变化，也就是常见的微积分思想

由此，也可以将微分形推广到更高维的情况

定义 Rn\mathbb R^n 上的 1 - 形式
令 U⊂RnU\subset\mathbb R^n 为开集
fi:U→R,fi∈C∞(U)(i=1,…,n)f_i:U \to \mathbb R,\quad f_i \in C^\infty(U) \quad (i=1,\dots,n)

与 p∈U,v∈TpU\boldsymbol p \in U, \boldsymbol v \in T_{\boldsymbol p}U 对应的函数

∑i=1nfidxi:TpU→R\sum_{i=1}^n f_idx_i: T_{\boldsymbol p}U \to \mathbb R

v→∑i=1nfi(p)dxi(v)\boldsymbol v \to \sum_{i=1}^n f_i(\boldsymbol p)dx_i(\boldsymbol v)

称为 U⊂RnU \subset \mathbb R^n 上的 C∞C^\infty 级 11 次微分形式

# 楔积

以下令 U⊂RnU\subset\mathbb R^n 为开集
UU 中的坐标记作 (x1,…,xn)(x_1,\dots,x_n)

定义
令 p∈Up \in U
i1,…,ik∈{1,…,n}i_1, \dots, i_k \in \{1, \dots, n\}
定义函数 dxi1∧dxi2∧⋯∧dxik:(TpU)k→Rdx_{i_1} \wedge dx_{i_2} \wedge \cdots \wedge dx_{i_k}: (T_pU)^k \to \mathbb R

(dxi1∧dxi2∧⋯∧dxik)(v1,…,vk):=∣dxi1(v1)⋯dxi1(vk)dxi2(v1)⋯dxi2(vk)⋮⋮dxik(v1)⋯dxik(vk)∣⁣.\bigl(dx_{i_1} \wedge dx_{i_2} \wedge \cdots \wedge dx_{i_k}\bigr)(v_1,\dots,v_k) :=\begin{vmatrix} dx_{i_1}(v_1) & \cdots & dx_{i_1}(v_k)\\ dx_{i_2}(v_1) & \cdots & dx_{i_2}(v_k)\\ \vdots & & \vdots\\ dx_{i_k}(v_1) & \cdots & dx_{i_k}(v_k) \end{vmatrix}\!.

为 dxi1,…,dxikdx_{i_1},\dots,dx_{i_k} 的 楔积 (wedge product)

楔积的常见计算类型如下

二维空间中的两元楔积计算，n=2n = 2，v=(v1,v2),w=(w1,w2)\boldsymbol v = (v_1, v_2),\ \boldsymbol w = (w_1, w_2)

(dx∧dy)(v,w)=∣dx(v)dx(w)dy(v)dy(w)∣=∣v1w1v2w2∣=v1w2−v2w1(dx \wedge dy)(\boldsymbol v,\boldsymbol w) = \begin{vmatrix} dx(\boldsymbol v) & dx(\boldsymbol w)\\ dy(\boldsymbol v) & dy(\boldsymbol w) \end{vmatrix} = \begin{vmatrix} v_1 & w_1 \\ v_2 & w_2 \end{vmatrix} = v_1 w_2 - v_2 w_1

其绝对值等于由 v,wv,w 张成的平行四边形面积。

S=∣v1w2−v2w1∣S = \left|v_1 w_2 - v_2 w_1\right|

三维空间中的两元楔积计算，n=3n = 3，v=(v1,v2,v3),w=(w1,w2,w3)v = (v_1, v_2, v_3),\ w = (w_1, w_2, w_3)

(dx∧dy)(v,w)=∣dx(v)dx(w)dy(v)dy(w)∣=∣v1w1v2w2∣=v1w2−v2w1(dx \wedge dy)(v, w) = \begin{vmatrix} dx(\boldsymbol v) & dx(\boldsymbol w)\\ dy(\boldsymbol v) & dy(\boldsymbol w) \end{vmatrix} = \begin{vmatrix} v_1 & w_1 \\ v_2 & w_2 \end{vmatrix} = v_1 w_2 - v_2 w_1

(dz∧dy)(v,w)=∣dz(v)dz(w)dy(v)dy(w)∣=∣v3w3v2w2∣=v3w2−v2w3(dz \wedge dy)(\boldsymbol v,\boldsymbol w) = \begin{vmatrix} dz(\boldsymbol v) & dz(\boldsymbol w)\\ dy(\boldsymbol v) & dy(\boldsymbol w) \end{vmatrix} = \begin{vmatrix} v_3 & w_3 \\ v_2 & w_2 \end{vmatrix} = v_3 w_2 - v_2 w_3

三维空间中的三元楔积计算，n=3n = 3，v=(v1,v2,v3),w=(w1,w2,w3),u=(u1,u2,u3)v = (v_1, v_2, v_3),\ w = (w_1, w_2, w_3),\ u = (u_1, u_2, u_3)

(dx∧dy∧dz)(v,w,u)=∣dx(v)dx(w)dx(u)dy(v)dy(w)dy(u)dz(v)dz(w)dz(u)∣=∣v1w1u1v2w2u2v3w3u3∣(dx \wedge dy \wedge dz)(v, w, u) = \begin{vmatrix} dx(\boldsymbol v) & dx(\boldsymbol w) & dx(\boldsymbol u)\\ dy(\boldsymbol v) & dy(\boldsymbol w) & dy(\boldsymbol u)\\ dz(\boldsymbol v) & dz(\boldsymbol w) & dz(\boldsymbol u) \end{vmatrix} = \begin{vmatrix} v_1 & w_1 & u_1\\ v_2 & w_2 & u_2\\ v_3 & w_3 & u_3 \end{vmatrix}

因为楔积的计算基于行列式定义，而行列式的行列交换具有交代性，所以交换奇数次楔积因子会变为负号，交换偶数次楔积因子不变
例如

dx∧dy∧dz∧dk=−dx∧dz∧dy∧dkdx \wedge dy \wedge dz \wedge dk = - dx \wedge dz \wedge dy \wedge dk

dx∧dy∧dz∧dk=dx∧dz∧dk∧dydx \wedge dy \wedge dz \wedge dk = dx \wedge dz \wedge dk \wedge dy

同时，如果行列式中存在相同的行或者列，则行列式值为零。楔积也继承了这个性质

dx∧dx=0,dy∧dy=0,dz∧dz=0dx \wedge dx = 0,\quad dy \wedge dy = 0,\quad dz \wedge dz = 0

dx∧dy∧dz∧dx=0dx \wedge dy \wedge dz \wedge dx = 0

注意：如果楔积因子的数量超过了空间的维度，则必然存在重复的因子，楔积结果为零

# kk 形式

引入楔积，得以定义更高次的微分形

定义 Rn\mathbb R^n 上的 kk 形式
令 U⊂RnU \subset \mathbb R^n 为开集
p∈U\boldsymbol p \in U
i1,…,ik∈{1,2,…,n}i_1, \dots, i_k \in \{1, 2, \dots, n\}
fi:U→R,fi∈C∞(U)(i=1,…,n)f_i:U \to \mathbb R,\quad f_i \in C^\infty(U) \quad (i=1,\dots,n)

称与 p∈U,vi∈TpU\boldsymbol p \in U, \boldsymbol v_i \in T_{\boldsymbol p}U 对应的函数

ω:(TpU)k→R\omega: (T_{\boldsymbol p}U)^k \to \mathbb R

ω:=∑i1,…,ik=1nfi1⋯ikdxi1∧⋯∧dxik\omega:=\sum_{i_1,\dots,i_k=1}^n f_{i_1\cdots i_k}\;dx_{i_1}\wedge\cdots\wedge dx_{i_k}

为 UU 上的 C∞C^\infty 级 kk 次微分形式
或者称为 kk 形式 (k-form)「kk 形式」

其在点 p\boldsymbol p 处，(v1,…,vk)(\boldsymbol v_1, \dots, \boldsymbol v_k) 的取值记为 ωp(v1,…,vk)\omega_{\boldsymbol p}(\boldsymbol v_1,\dots,\boldsymbol v_k)。

特别地，称 C∞C^\infty 级函数 f:U→Rf:U \to \mathbb R 为 UU 上的 00 形式

记 UU 上所有 kk 形式的集合为 Ωk(U)\Omega^k(U)。

为避免混淆，提醒：

  • ω\omega 是一个函数，自变量为切空间中的数个向量，映射为实数
  • p\boldsymbol p 是 UU 中的一个定点，切空间和 ω\omega 都是依赖于这个点来定义的，不同的定点会得到不同的切空间和 ω\omega
  • ωp\omega_{\boldsymbol p} 是 ω\omega 在点 p\boldsymbol p 处具体的取值，是实数
  • fi:U→Rf_i:U \to \mathbb R 是坐标函数，数量等于空间维度

kk 形式的常见计算类型如下，注意各个计算中利用楔积的性质进行简化

二维空间中的 2 - 形式，n=2,k=2n = 2, k = 2

ω=f11dx∧dx+f12dx∧dy+f21dy∧dx+f22dy∧dy=(f12−f21)dx∧dy\begin{aligned} \omega &= f_{11} dx \wedge dx + f_{12} dx \wedge dy + f_{21} dy \wedge dx + f_{22} dy \wedge dy \\ &= (f_{12} - f_{21}) dx \wedge dy \end{aligned}

三维空间中的 2 - 形式，n=3,k=2n = 3, k = 2

ω=f11dx∧dx+f12dx∧dy+f13dx∧dz+f21dy∧dx+f22dy∧dy+f23dy∧dz+f31dz∧dx+f32dz∧dy+f33dz∧dz=(f12−f21)dx∧dy+(f13−f31)dz∧dx+(f23−f32)dy∧dz\begin{aligned} \omega &= f_{11} dx \wedge dx + f_{12} dx \wedge dy + f_{13} dx \wedge dz \\ &\quad + f_{21} dy \wedge dx + f_{22} dy \wedge dy + f_{23} dy \wedge dz \\ &\quad + f_{31} dz \wedge dx + f_{32} dz \wedge dy + f_{33} dz \wedge dz \\ &= (f_{12} - f_{21}) dx \wedge dy + (f_{13} - f_{31}) dz \wedge dx + (f_{23} - f_{32}) dy \wedge dz \end{aligned}

三维空间中的 3 - 形式，n=3,k=3n = 3, k = 3

ω=f111dx∧dx∧dx+f112dx∧dx∧dy+f113dx∧dx∧dz+f121dx∧dy∧dx+f122dx∧dy∧dy+f123dx∧dy∧dz+f131dx∧dz∧dx+f132dx∧dz∧dy+f133dx∧dz∧dz+f211dy∧dx∧dx+f212dy∧dx∧dy+f213dy∧dx∧dz+f221dy∧dy∧dx+f222dy∧dy∧dy+f223dy∧dy∧dz+f231dy∧dz∧dx+f232dy∧dz∧dy+f233dy∧dz∧dz+f311dz∧dx∧dx+f312dz∧dx∧dy+f313dz∧dx∧dz+f321dz∧dy∧dx+f322dz∧dy∧dy+f323dz∧dy∧dz+f331dz∧dz∧dx+f332dz∧dz∧dy+f333dz∧dz∧dz=(f123+f231+f312−f132−f213−f321)dx∧dy∧dz\begin{aligned} \omega &= f_{111} dx \wedge dx \wedge dx + f_{112} dx \wedge dx \wedge dy + f_{113} dx \wedge dx \wedge dz \\ &\quad + f_{121} dx \wedge dy \wedge dx + f_{122} dx \wedge dy \wedge dy + f_{123} dx \wedge dy \wedge dz \\ &\quad + f_{131} dx \wedge dz \wedge dx + f_{132} dx \wedge dz \wedge dy + f_{133} dx \wedge dz \wedge dz \\ &\quad + f_{211} dy \wedge dx \wedge dx + f_{212} dy \wedge dx \wedge dy + f_{213} dy \wedge dx \wedge dz \\ &\quad + f_{221} dy \wedge dy \wedge dx + f_{222} dy \wedge dy \wedge dy + f_{223} dy \wedge dy \wedge dz \\ &\quad + f_{231} dy \wedge dz \wedge dx + f_{232} dy \wedge dz \wedge dy + f_{233} dy \wedge dz \wedge dz \\ &\quad + f_{311} dz \wedge dx \wedge dx + f_{312} dz \wedge dx \wedge dy + f_{313} dz \wedge dx \wedge dz \\ &\quad + f_{321} dz \wedge dy \wedge dx + f_{322} dz \wedge dy \wedge dy + f_{323} dz \wedge dy \wedge dz \\ &\quad + f_{331} dz \wedge dz \wedge dx + f_{332} dz \wedge dz \wedge dy + f_{333} dz \wedge dz \wedge dz \\ &= (f_{123} + f_{231} + f_{312} - f_{132} - f_{213} - f_{321}) dx \wedge dy \wedge dz \end{aligned}

重点结论
由此可知，任意一般情况下 nn 维空间中的 kk 形式都可以化简为

ω=∑1≤i1<i2<⋯<ik≤nhi1⋯ikdxi1∧dxi2∧⋯∧dxik\omega = \sum_{1 \le i_1 < i_2 < \cdots < i_k \le n} h_{i_1 \cdots i_k} dx_{i_1} \wedge dx_{i_2} \wedge \cdots \wedge dx_{i_k}

其中 hi1⋯ik∈C∞(U)h_{i_1 \cdots i_k} \in C^\infty(U)
也就是说右侧楔积的部分都可以化简为一个固定的顺序

微分形之间可以定义加法与标量乘法，并且满足线性
（就如同先前所说：将非线性变成转为线性进行分析）

令 α,β∈Ωk(U),h∈C∞(U)\alpha, \beta \in \Omega^k(U),\ h \in C^\infty(U)

  • 加法 α+β\alpha + \beta 定义为（结果为 kk 形式）

(α+β)p(v1,…,vk)=αp(v1,…,vk)+βp(v1,…,vk)(\alpha + \beta)_p(v_1, \dots, v_k) = \alpha_p(v_1, \dots, v_k) + \beta_p(v_1, \dots, v_k)

  • 标量乘法 hαh\alpha 定义为（结果为 kk 形式）

(hα)p(v1,…,vk)=h(p)αp(v1,…,vk)(h\alpha)_p(v_1, \dots, v_k) = h(p) \alpha_p(v_1, \dots, v_k)

由此 Ωk(U)\Omega^k(U) 在加法与函数倍下构成（无限维）实向量空间