几何中的曲线在分析角度本质上是一个向量函数。
从 R 中取区间 I,用 t 表示区间中的变量
那么曲线就可以表示为
c:I→Rn, t↦c(t)
# 正则曲线
定义
若对于任意 t∈I
c′(t)=0
则称 c 为 正则曲线 (regular curve)。
在值域中,n=2 时称为平面曲线,n=3 时称为空间曲线。实际上研究的是任意维度下的曲线
可以将曲线理解为一个路径,或者说是运动轨迹
参数 t 可以理解为时间
随着时间的增加,向量 c(t) 的终点会在空间中描绘出这条曲线,或者也可以说有一个小质点在沿着这个曲线运动
既然谈到运动,自然会有速度
定义
曲线 c 的微分
c′(t)=dtdc=(dtdx1,dtdx2,⋯,dtdxn)
称为曲线 c 的 * 切向量 (tangent vector),或者叫 速度向量 (velocity vector)
并且
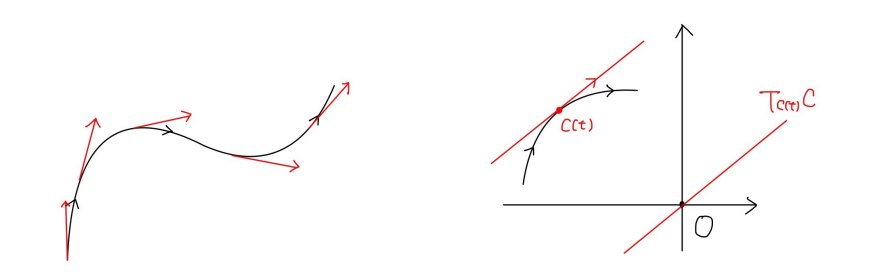
Tc(t)c={λc′(t)∣λ∈R}
称为曲线 c 在点 c(t) 处的 切空间 (tangent space)。
虽然切向量本身是 Rn 中的向量(以原点为起点的),但是往往在研究过程中,会将它平移到曲线的那个点上作为起点,视为几何向量
切空间也是一样的
![切向量与切空间]()
那在作为路径的理解上,可以将正则曲线简单翻译为:一条连续并且是真的能靠一辆车开出来的路径
(在非正则点上,也就是 c′(t)=0,也叫做奇点,路径会有很尖锐的瞬间变化,车是开不出来的)
注意:正则曲线并不要求单射,所以允许交叉
# 曲线的长度
那么考虑一下要如何计算曲线的长度
数学分析中已经非常熟悉了积分的概念:将一个量分割成无数个小份,然后将这些小份加起来
曲线的长度也可以用同样的思路来计算
想象一下在曲线上的一个点,它具有一个速度,那么在极短时间 Δt 内,这个点大致会移动的距离就是
Δs≈∣c′(t)∣Δt
如果的时间间隔 Δt 足够小,那么移动的方向误差就会无关紧要
此时 Δs→ds,对其积分就可以得到
定义
对于可微曲线 c:[a,b]→Rn,称
L(c)=∫ab∣c′(t)∣dt
为曲线 c 的 长度 (length)
现在拥有了曲线的长度,可以进入整个曲线分析最核心的概念了:弧长参数化
弧长参数化本质上是通过赋予曲线一个新的变量,从而使得曲线的变化速率恒定一致
定义
令正则曲线 c:[a,b]→Rn
长度 ℓ=L(c)
定义映射
s:[a,b]→[0,ℓ],s(t)=∫at∣c′(t)∣dt
称 s 为曲线 c 的 弧长参数 (arc length parameter)。
正则性给出 s 单调递增,所以存在反函数
t:[0,ℓ]→[a,b],t(s)=s−1(t)
此时称新的曲线
c~:[0,ℓ]→Rn,c~(s)=(c∘t)(s)
为曲线 c 的 弧长参数化 (arc length parameterization)。
弧长参数化具有以下性质
命题
对于弧长参数化的曲线 \tilde
∣c~′(s)∣=1
且对于任意 s0∈[0,l],曲线 c~∣[0,s0] 的长度都为 s0
证明
由链式法则,注意求导为对 s 求导
c~′(s)=c′(t(s))⋅t′(s)
由反函数求导公式
t′(s)=s′(t(s))1=∣c′(t(s))∣1
所以
∣c~′(s)∣=∣c′(t(s))∣⋅∣t′(s)∣=∣c′(t(s))∣⋅∣c′(t(s))∣1=1
另外,对于任意 s0∈[0,ℓ],由长度定义
L(c~∣[0,s0])=∫0s0∣c~′(s)∣ds=∫0s01ds=s0
今后对于曲线的所有的性质的研究,基本上都是基于弧长参数化的曲线
示例
考虑曲线
c(t)=⎝⎜⎜⎜⎜⎜⎛1+t21−t21+t22t0⎠⎟⎟⎟⎟⎟⎞,t∈R
计算其弧长参数化
解
计算切向量
c′(t)=⎝⎜⎜⎜⎜⎜⎛−(1+t2)22t(1+t2)22(1+t2)−4t20⎠⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎛−(1+t2)22t(1+t2)22(1−t2)0⎠⎟⎟⎟⎟⎟⎞
弧长参数
s(t)=∫0t∣c′(τ)∣dτ=∫0t1+τ22dτ=2arctant
反函数
t(s)=tan2s
代入得到弧长参数化
c~(s)=c(t(s))=⎝⎜⎜⎜⎜⎜⎜⎛1+tan22s1−tan22s1+tan22s2tan2s0⎠⎟⎟⎟⎟⎟⎟⎞=⎝⎛cosssins0⎠⎞