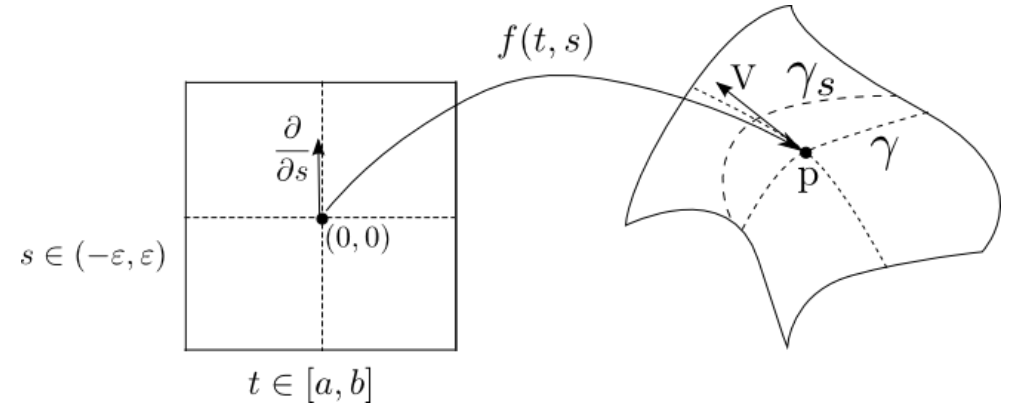
以下令 S S S
# 测地线定义 S S S C ∞ C^\infty C ∞ γ : I → S \boldsymbol \gamma : I \to S γ : I → S
d 2 γ d t 2 ⊥ T γ ( t ) S , ∀ t ∈ I \frac{d^2 \boldsymbol \gamma}{dt^2} \perp T_{\boldsymbol \gamma(t)}S,\ \forall t \in I \quad d t 2 d 2 γ ⊥ T γ ( t ) S , ∀ t ∈ I
则称 γ \boldsymbol \gamma γ S S S 测地线 (Geodesic)「測地線」
命题 γ : I → R 3 \boldsymbol \gamma:I \to \mathbb R^3 γ : I → R 3 S S S
∥ γ ′ ( t ) ∥ = 常数 \|\boldsymbol \gamma'(t)\| = \text{常数} \quad ∥ γ ′ ( t ) ∥ = 常数 γ ~ ( s ) : = γ ( s λ ) \boldsymbol{\tilde \gamma(s)} := \boldsymbol \gamma (\frac{s}{\lambda}) γ ~ ( s ) : = γ ( λ s ) λ = ∥ γ ′ ( t 0 ) ∥ ≠ 0 \lambda = \|\boldsymbol \gamma'(t_0)\| \neq 0 \quad λ = ∥ γ ′ ( t 0 ) ∥ = 0 证明 (1) 由于 γ ′ ∈ T γ ( t ) S \boldsymbol \gamma' \in T_{\boldsymbol \gamma(t)}S γ ′ ∈ T γ ( t ) S
0 = γ ′ ′ ⋅ γ ′ = 1 2 d d t ( γ ′ ⋅ γ ′ ) = d d t ∥ γ ′ ( t ) ∥ 2 0 = \boldsymbol \gamma'' \cdot \boldsymbol \gamma' = \frac{1}{2} \frac{d}{dt} \left(\boldsymbol \gamma' \cdot \boldsymbol \gamma'\right) = \frac{d}{dt} \|\boldsymbol \gamma'(t)\|^2 0 = γ ′ ′ ⋅ γ ′ = 2 1 d t d ( γ ′ ⋅ γ ′ ) = d t d ∥ γ ′ ( t ) ∥ 2
(2)
d 2 γ ~ d s 2 ( s ) = d 2 γ d s 2 ( s λ ) = 1 λ 2 d 2 γ d t 2 ( s λ ) ⊥ T γ ( s λ ) S = T γ ~ ( s ) S \frac{d^2 \boldsymbol{\tilde \gamma}}{ds^2}(s) = \frac{d^2 \boldsymbol \gamma}{ds^2}(\frac{s}{\lambda}) = \frac{1}{\lambda^2} \frac{d^2 \boldsymbol \gamma}{dt^2}(\frac{s}{\lambda}) \perp T_{\boldsymbol \gamma(\frac{s}{\lambda})}S = T_{\boldsymbol{\tilde \gamma}(s)}S d s 2 d 2 γ ~ ( s ) = d s 2 d 2 γ ( λ s ) = λ 2 1 d t 2 d 2 γ ( λ s ) ⊥ T γ ( λ s ) S = T γ ~ ( s ) S
示例 S ⊂ R 3 S \subset \mathbb R^3 S ⊂ R 3 v ∈ R 3 \boldsymbol v \in \mathbb R^3 v ∈ R 3 p ∈ S \boldsymbol p \in S p ∈ S γ ( t ) = p + t v \boldsymbol \gamma(t) = \boldsymbol p + t\boldsymbol v γ ( t ) = p + t v S S S
证明 显而易见 γ ′ ′ = 0 ⊥ T γ ( t ) S \boldsymbol \gamma'' = 0 \perp T_{\boldsymbol \gamma(t)}S γ ′ ′ = 0 ⊥ T γ ( t ) S
示例 S = S 2 ( r ) ⊂ R 3 S = S^2(r) \subset \mathbb R^3 S = S 2 ( r ) ⊂ R 3
γ ( t ) = ( r cos t r sin t 0 ) , t ∈ R \boldsymbol \gamma(t) = \begin{pmatrix} r \cos t \\ r \sin t \\ 0 \end{pmatrix}, \quad t \in \mathbb R γ ( t ) = ⎝ ⎛ r cos t r sin t 0 ⎠ ⎞ , t ∈ R
为 S S S
证明 计算可得
γ ′ ′ ( t ) = ( − r cos t − r sin t 0 ) = − 1 r γ ( t ) \boldsymbol \gamma''(t) = \begin{pmatrix} -r \cos t \\ -r \sin t \\ 0 \end{pmatrix} = -\frac{1}{r} \boldsymbol \gamma(t) γ ′ ′ ( t ) = ⎝ ⎛ − r cos t − r sin t 0 ⎠ ⎞ = − r 1 γ ( t )
与
n ( γ ( t ) ) = ( cos t sin t 0 ) \boldsymbol n(\boldsymbol \gamma(t)) = \begin{pmatrix} \cos t \\ \sin t \\ 0 \end{pmatrix} n ( γ ( t ) ) = ⎝ ⎛ cos t sin t 0 ⎠ ⎞
平行,所以 γ ′ ′ ( t ) ⊥ T γ ( t ) S \boldsymbol \gamma''(t) \perp T_{\boldsymbol \gamma(t)}S γ ′ ′ ( t ) ⊥ T γ ( t ) S
# 参数化下的测地线推导取 S S S σ : D → R 3 \boldsymbol \sigma: D \to \mathbb R^3 σ : D → R 3 ( u 1 , u 2 ) = ( u , v ) (u^1,u^2) = (u,v) ( u 1 , u 2 ) = ( u , v )
σ 1 = σ u \boldsymbol \sigma_1 = \boldsymbol \sigma_u σ 1 = σ u σ 2 = σ v \boldsymbol \sigma_2 = \boldsymbol \sigma_v σ 2 = σ v σ 11 = σ u u \boldsymbol \sigma_{11} = \boldsymbol \sigma_{uu} \quad σ 1 1 = σ u u σ 12 = σ u v \boldsymbol \sigma_{12} = \boldsymbol \sigma_{uv} \quad σ 1 2 = σ u v σ 22 = σ v v \boldsymbol \sigma_{22} = \boldsymbol \sigma_{vv} \quad σ 2 2 = σ v v 取 Riemannian 度规 g i j = σ i ⋅ σ j g_{ij} = \boldsymbol \sigma_i \cdot \boldsymbol \sigma_j g i j = σ i ⋅ σ j h i j = σ i j ⋅ n , i , j = 1 , 2 h_{ij} = \boldsymbol \sigma_{ij} \cdot \boldsymbol n,\quad i,j = 1,2 h i j = σ i j ⋅ n , i , j = 1 , 2
( g i j ) = ( E F F G ) , ( h i j ) = ( L M N G ) (g_{ij}) = \begin{pmatrix} E & F \\ F & G \end{pmatrix},\quad (h_{ij}) = \begin{pmatrix} L & M \\ N & G \end{pmatrix} ( g i j ) = ( E F F G ) , ( h i j ) = ( L N M G )
注意 g i j = g j i g_{ij} = g_{ji} g i j = g j i h i j = h j i h_{ij} = h_{ji} \quad h i j = h j i
逆矩阵
( g i j ) = ( g i j ) − 1 = 1 E G − F 2 ( G − F − F E ) (g^{ij}) = (g_{ij})^{-1} = \frac{1}{EG - F^2} \begin{pmatrix} G & -F \\ -F & E \end{pmatrix} ( g i j ) = ( g i j ) − 1 = E G − F 2 1 ( G − F − F E )
的 ( i , j ) (i,j) ( i , j ) g i j g^{ij} \quad g i j
此时 σ 1 , σ 2 , n \boldsymbol \sigma_1,\boldsymbol \sigma_2,\boldsymbol n σ 1 , σ 2 , n R 3 \mathbb R^3 R 3
所以可以将 σ j k \boldsymbol \sigma_{jk} σ j k
σ j k = Γ j k 1 σ 1 + Γ j k 2 σ 2 + Γ j k 3 n , j , k = 1 , 2 \boldsymbol \sigma_{jk} = \Gamma_{jk}^1 \boldsymbol \sigma_1 + \Gamma_{jk}^2 \boldsymbol \sigma_2 + \Gamma_{jk}^3 \boldsymbol n,\quad j,k = 1,2 σ j k = Γ j k 1 σ 1 + Γ j k 2 σ 2 + Γ j k 3 n , j , k = 1 , 2
由于
Γ j k 3 = σ j k ⋅ n = h j k \Gamma_{jk}^3 = \boldsymbol \sigma_{jk} \cdot \boldsymbol n = h_{jk} Γ j k 3 = σ j k ⋅ n = h j k
所以改写为
σ j k = Γ j k 1 σ 1 + Γ j k 2 σ 2 + h j k n , j , k = 1 , 2 \boldsymbol \sigma_{jk} = \Gamma_{jk}^1 \boldsymbol \sigma_1 + \Gamma_{jk}^2 \boldsymbol \sigma_2 + h_{jk} \boldsymbol n,\quad j,k = 1,2 σ j k = Γ j k 1 σ 1 + Γ j k 2 σ 2 + h j k n , j , k = 1 , 2
其中 Γ j k i \Gamma_{jk}^i Γ j k i Christoffel 符号 (Christoffel Symbol)「クリストッフェル記号」
注意继承于 σ j k = σ k j \boldsymbol \sigma_{jk} = \boldsymbol \sigma_{kj} σ j k = σ k j Γ j k i = Γ k j i \Gamma_{jk}^i = \Gamma_{kj}^i Γ j k i = Γ k j i
那么对于满足 γ ( t ) ∈ σ ( D ) \boldsymbol \gamma(t) \in \boldsymbol \sigma(D) γ ( t ) ∈ σ ( D ) t ∈ R t \in \mathbb R t ∈ R γ \boldsymbol \gamma γ
γ ( t ) = σ ( u 1 ( t ) , u 2 ( t ) ) \boldsymbol \gamma(t) = \boldsymbol \sigma(u^1(t),u^2(t)) γ ( t ) = σ ( u 1 ( t ) , u 2 ( t ) )
则
d γ d t ( t ) = ∑ j = 1 2 σ j ( u 1 ( t ) , u 2 ( t ) ) d u j d t ( t ) \frac{d \boldsymbol \gamma}{dt}(t) = \sum_{j=1}^2 \boldsymbol \sigma_j(u^1(t),u^2(t)) \frac{du^j}{dt}(t) d t d γ ( t ) = j = 1 ∑ 2 σ j ( u 1 ( t ) , u 2 ( t ) ) d t d u j ( t )
d 2 γ d t 2 ( t ) = ∑ j , k = 1 2 σ j k ( u 1 ( t ) , u 2 ( t ) ) d u j d t ( t ) d u k d t ( t ) + ∑ j = 1 2 σ j ( u 1 ( t ) , u 2 ( t ) ) d 2 u j d t 2 ( t ) = ∑ i , j , k = 1 2 Γ j k i σ i d u j d t d u k d t + ∑ j = 1 2 σ j d 2 u j d t 2 + ( ∑ j , k = 1 2 h j k d u j d t d u k d t ) n = ∑ i = 1 2 ( ∑ j , k = 1 2 Γ j k i ( u 1 ( t ) , u 2 ( t ) ) d u j d t ( t ) d u k d t ( t ) + d 2 u i d t 2 ( t ) ) ⏟ 切向分量 σ i ( u 1 ( t ) , u 2 ( t ) ) + ( ∑ j , k = 1 2 h j k ( u 1 ( t ) , u 2 ( t ) ) d u j d t ( t ) d u k d t ( t ) ) ⏟ 法向分量 n ( u 1 ( t ) , u 2 ( t ) ) \begin{aligned} \frac{d^2 \boldsymbol \gamma}{dt^2}(t) &= \sum_{j,k=1}^2 \boldsymbol \sigma_{jk}(u^1(t),u^2(t)) \frac{du^j}{dt}(t) \frac{du^k}{dt}(t) + \sum_{j=1}^2 \boldsymbol \sigma_j(u^1(t),u^2(t)) \frac{d^2 u^j}{dt^2}(t) \\ &= \sum_{i,j,k=1}^2 \Gamma_{jk}^i \boldsymbol \sigma_i \frac{du^j}{dt} \frac{du^k}{dt} + \sum_{j=1}^2 \boldsymbol \sigma_j \frac{d^2 u^j}{dt^2} + \left( \sum_{j,k=1}^2 h_{jk} \frac{du^j}{dt} \frac{du^k}{dt} \right) \boldsymbol n \\ &= \underbrace{ \sum_{i=1}^2 \left( \sum_{j,k=1}^2 \Gamma_{jk}^i(u^1(t),u^2(t)) \frac{du^j}{dt}(t) \frac{du^k}{dt}(t) + \frac{d^2 u^i}{dt^2}(t) \right) }_{\text{切向分量}} \boldsymbol \sigma_i(u^1(t),u^2(t)) \\ &+ \underbrace{ \left( \sum_{j,k=1}^2 h_{jk}(u^1(t),u^2(t)) \frac{du^j}{dt}(t) \frac{du^k}{dt}(t) \right) }_{\text{法向分量}} \boldsymbol n(u^1(t),u^2(t) ) \end{aligned} d t 2 d 2 γ ( t ) = j , k = 1 ∑ 2 σ j k ( u 1 ( t ) , u 2 ( t ) ) d t d u j ( t ) d t d u k ( t ) + j = 1 ∑ 2 σ j ( u 1 ( t ) , u 2 ( t ) ) d t 2 d 2 u j ( t ) = i , j , k = 1 ∑ 2 Γ j k i σ i d t d u j d t d u k + j = 1 ∑ 2 σ j d t 2 d 2 u j + ⎝ ⎛ j , k = 1 ∑ 2 h j k d t d u j d t d u k ⎠ ⎞ n = 切向分量 i = 1 ∑ 2 ⎝ ⎛ j , k = 1 ∑ 2 Γ j k i ( u 1 ( t ) , u 2 ( t ) ) d t d u j ( t ) d t d u k ( t ) + d t 2 d 2 u i ( t ) ⎠ ⎞ σ i ( u 1 ( t ) , u 2 ( t ) ) + 法向分量 ⎝ ⎛ j , k = 1 ∑ 2 h j k ( u 1 ( t ) , u 2 ( t ) ) d t d u j ( t ) d t d u k ( t ) ⎠ ⎞ n ( u 1 ( t ) , u 2 ( t ) )
由于 σ i ⊥ T γ ( t ) S , n ⊥ T γ ( t ) S \boldsymbol \sigma_i \perp T_{\boldsymbol \gamma(t)}S, \quad \boldsymbol n \perp T_{\boldsymbol \gamma(t)}S σ i ⊥ T γ ( t ) S , n ⊥ T γ ( t ) S γ \boldsymbol \gamma γ
d 2 γ d t 2 ⊥ T γ ( t ) S ⟺ d 2 u i d t 2 + ∑ j , k = 1 2 Γ j k i d u j d t d u k d t = 0 ⏟ 关于 u i ( t ) 的 2 阶常微分方程 , i = 1 , 2 \frac{d^2 \boldsymbol \gamma}{dt^2} \perp T_{\boldsymbol \gamma(t)}S \iff \underbrace{ \frac{d^2 u^i}{dt^2} + \sum_{j,k=1}^2 \Gamma_{jk}^i \frac{du^j}{dt} \frac{du^k}{dt} = 0 }_{\text{关于 $u^i(t)$ 的 $2$ 阶常微分方程}},\quad i = 1,2 d t 2 d 2 γ ⊥ T γ ( t ) S ⟺ 关于 u i ( t ) 的 2 阶常微分方程 d t 2 d 2 u i + j , k = 1 ∑ 2 Γ j k i d t d u j d t d u k = 0 , i = 1 , 2
关于常微分方程组的解的存在唯一性可由常微分方程基本定理保证
命题 p ∈ S \boldsymbol p \in S p ∈ S v ∈ T p S \boldsymbol v \in T_{\boldsymbol p}S v ∈ T p S δ > 0 \delta \gt 0 δ > 0 γ : ( − δ , δ ) → S \boldsymbol \gamma:(-\delta,\delta) \to S γ : ( − δ , δ ) → S
γ ( 0 ) = p , γ ′ ( 0 ) = v \boldsymbol \gamma(0) = \boldsymbol p,\quad \boldsymbol \gamma'(0) = \boldsymbol v γ ( 0 ) = p , γ ′ ( 0 ) = v
命题
Γ j k i = 1 2 ∑ m = 1 2 g i m ( ∂ g m k ∂ u j + ∂ g m j ∂ u k − ∂ g j k ∂ u m ) \Gamma_{jk}^i = \frac{1}{2} \sum_{m=1}^2 g^{im} \left( \frac{\partial g_{mk}}{\partial u^j} + \frac{\partial g_{mj}}{\partial u^k} - \frac{\partial g_{jk}}{\partial u^m} \right) Γ j k i = 2 1 m = 1 ∑ 2 g i m ( ∂ u j ∂ g m k + ∂ u k ∂ g m j − ∂ u m ∂ g j k )
证明 由 g i j = σ i ⋅ σ j g_{ij} = \boldsymbol \sigma_i \cdot \boldsymbol \sigma_j g i j = σ i ⋅ σ j
∂ g j k ∂ u l = σ j l ⋅ σ k + σ j ⋅ σ k l \frac{\partial g_{jk}}{\partial u^l} = \boldsymbol \sigma_{jl} \cdot \boldsymbol \sigma_k + \boldsymbol \sigma_j \cdot \boldsymbol \sigma_{kl} ∂ u l ∂ g j k = σ j l ⋅ σ k + σ j ⋅ σ k l
将 σ i j \boldsymbol \sigma_{ij} σ i j
∂ g j k ∂ u l = ∑ m = 1 2 Γ j l m g m k + ∑ m = 1 2 Γ k l m g m j \frac{\partial g_{jk}}{\partial u^l} = \sum_{m=1}^2 \Gamma_{jl}^m g_{mk} + \sum_{m=1}^2 \Gamma_{kl}^m g_{mj} ∂ u l ∂ g j k = m = 1 ∑ 2 Γ j l m g m k + m = 1 ∑ 2 Γ k l m g m j
交换 j , k , l j,k,l j , k , l
{ ∂ g k l ∂ u j = ∑ i = 1 2 Γ k j i g i l ‾ + ∑ i = 1 2 Γ l j i g i k ‾ ∂ g k l ∂ u j = ∑ i = 1 2 Γ l k i g i j ‾ + ∑ i = 1 2 Γ j k i g i l ‾ ∂ g k j ∂ u l = ∑ i = 1 2 Γ k j i g i l ‾ + ∑ i = 1 2 Γ j l i g i k ‾ \begin{cases} \frac{\partial g_{kl}}{\partial u^j} = \textcolor{yellow}{\underline{\textcolor{lightgrey}{\sum_{i=1}^2 \Gamma_{kj}^i g_{il}}}} + \textcolor{pink}{\underline{\textcolor{lightgrey}{\sum_{i=1}^2 \Gamma_{lj}^i g_{ik}}}} \\ \frac{\partial g_{kl}}{\partial u^j} = \textcolor{pink}{\underline{\textcolor{lightgrey}{\sum_{i=1}^2 \Gamma_{lk}^i g_{ij}}}} + \textcolor{cyan}{\underline{\textcolor{lightgrey}{\sum_{i=1}^2 \Gamma_{jk}^i g_{il}}}} \\ \frac{\partial g_{kj}}{\partial u^l} = \textcolor{yellow}{\underline{\textcolor{lightgrey}{\sum_{i=1}^2 \Gamma_{kj}^i g_{il}}}} + \textcolor{cyan}{\underline{\textcolor{lightgrey}{\sum_{i=1}^2 \Gamma_{jl}^i g_{ik}}}} \end{cases} ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ ∂ u j ∂ g k l = ∑ i = 1 2 Γ k j i g i l + ∑ i = 1 2 Γ l j i g i k ∂ u j ∂ g k l = ∑ i = 1 2 Γ l k i g i j + ∑ i = 1 2 Γ j k i g i l ∂ u l ∂ g k j = ∑ i = 1 2 Γ k j i g i l + ∑ i = 1 2 Γ j l i g i k
相加减后可得
∂ g m k ∂ u j + ∂ g m j ∂ u k − ∂ g j k ∂ u m = 2 ∑ i = 1 2 Γ j k i g i m \frac{\partial g_{mk}}{\partial u^j} + \frac{\partial g_{mj}}{\partial u^k} - \frac{\partial g_{jk}}{\partial u^m} = 2 \sum_{i=1}^2 \Gamma_{jk}^i g_{im} ∂ u j ∂ g m k + ∂ u k ∂ g m j − ∂ u m ∂ g j k = 2 i = 1 ∑ 2 Γ j k i g i m
两边同时乘以 g i m g^{im} g i m
∑ m = 1 2 g i m ( ∂ g m k ∂ u j + ∂ g m j ∂ u k − ∂ g j k ∂ u m ) = 2 ∑ i = 1 2 Γ j k i \sum_{m=1}^2 g^{im} \left( \frac{\partial g_{mk}}{\partial u^j} + \frac{\partial g_{mj}}{\partial u^k} - \frac{\partial g_{jk}}{\partial u^m} \right) = 2 \sum_{i=1}^2 \Gamma_{jk}^i m = 1 ∑ 2 g i m ( ∂ u j ∂ g m k + ∂ u k ∂ g m j − ∂ u m ∂ g j k ) = 2 i = 1 ∑ 2 Γ j k i
将此处算出的 Christoffel 符号代入
σ j k = ∑ i = 1 2 Γ j k i σ i + h j k n , j , k = 1 , 2 \boldsymbol \sigma_{jk} = \sum_{i=1}^2 \Gamma_{jk}^i \boldsymbol \sigma_i + h_{jk} \boldsymbol n,\quad j,k = 1,2 σ j k = i = 1 ∑ 2 Γ j k i σ i + h j k n , j , k = 1 , 2
所得公式称为 Gauss 公式 (Gauss Formula)「ガウスの公式」
# 协变微分令 γ : I → S \boldsymbol \gamma: I \to S γ : I → S S S S
定义 C ∞ C^\infty C ∞ X : I → R 3 \boldsymbol X: I \to R^3 X : I → R 3
X ( t ) ∈ T γ ( t ) S , ∀ t ∈ I \boldsymbol X(t) \in T_{\boldsymbol \gamma(t)}S,\ \forall t \in I X ( t ) ∈ T γ ( t ) S , ∀ t ∈ I
则称 X \boldsymbol X X S S S 沿曲线 γ \boldsymbol \gamma γ 一个 切向量场 (tangent vector field)「接ベクトル場」
示例 γ ′ ( t ) ∈ T γ ( t ) S \boldsymbol \gamma'(t) \in T_{\boldsymbol \gamma(t)}S γ ′ ( t ) ∈ T γ ( t ) S γ ′ \boldsymbol \gamma' γ ′ γ \boldsymbol \gamma γ
对于任意点 p ∈ S \boldsymbol p \in S p ∈ S v ∈ R 3 \boldsymbol v \in \mathbb R^3 v ∈ R 3 v \boldsymbol v v
v = v tan + v nor , v tan ∈ T p S , v nor ⊥ T p S \boldsymbol v = \boldsymbol v_{\text{tan}} + \boldsymbol v_{\text{nor}},\quad \boldsymbol v_{\text{tan}} \in T_{\boldsymbol p}S,\ \boldsymbol v_{\text{nor}} \perp T_{\boldsymbol p}S v = v tan + v nor , v tan ∈ T p S , v nor ⊥ T p S
其中
v nor = ( v ⋅ n ) n \boldsymbol v_{\text{nor}} = (\boldsymbol v \cdot \boldsymbol n) \boldsymbol n v nor = ( v ⋅ n ) n
v tan = v − ( v ⋅ n ) n \boldsymbol v_{\text{tan}} = \boldsymbol v - (\boldsymbol v \cdot \boldsymbol n) \boldsymbol n v tan = v − ( v ⋅ n ) n
定义 γ \boldsymbol \gamma γ X \boldsymbol X X
D X d t ( t ) = ( d X d t ( t ) ) tan = d X d t ( t ) − ( d X d t ( t ) ⋅ n ( γ ( t ) ) ) n ( γ ( t ) ) \frac{D\boldsymbol X}{dt}(t) = \left(\frac{d\boldsymbol X}{dt}(t)\right)_{\text{tan}} = \frac{d\boldsymbol X}{dt}(t) - \left(\frac{d\boldsymbol X}{dt}(t) \cdot \boldsymbol n(\boldsymbol \gamma(t))\right) \boldsymbol n(\boldsymbol \gamma(t)) d t D X ( t ) = ( d t d X ( t ) ) tan = d t d X ( t ) − ( d t d X ( t ) ⋅ n ( γ ( t ) ) ) n ( γ ( t ) )
为沿曲线 γ \boldsymbol \gamma γ X \boldsymbol X X 协变微分 (covariant derivative)「共変微分」
此时
X 沿曲线 γ 平行 ⟺ D X d t ( t ) = 0 , ∀ t ∈ I X \text{ 沿曲线 } \boldsymbol \gamma \text{ 平行 } \iff \frac{D\boldsymbol X}{dt}(t) = \boldsymbol 0,\ \forall t \in I X 沿曲线 γ 平行 ⟺ d t D X ( t ) = 0 , ∀ t ∈ I
示例
d γ ′ d t ( t ) = γ ′ ′ ( t ) ⊥ T γ ( t ) S \frac{d\boldsymbol \gamma'}{dt}(t) = \boldsymbol \gamma''(t) \perp T_{\boldsymbol \gamma(t)}S d t d γ ′ ( t ) = γ ′ ′ ( t ) ⊥ T γ ( t ) S
所以
γ 为 S 上的测地线 ⟺ D γ ′ d t ( t ) = 0 , ∀ t ∈ I ⟺ γ 沿曲线 γ 平行 \boldsymbol \gamma \text{ 为 } S \text{ 上的测地线 } \iff \frac{D\boldsymbol \gamma'}{dt}(t) = \boldsymbol 0,\ \forall t \in I \iff \boldsymbol \gamma \text{ 沿曲线 } \boldsymbol \gamma \text{ 平行 } γ 为 S 上的测地线 ⟺ d t D γ ′ ( t ) = 0 , ∀ t ∈ I ⟺ γ 沿曲线 γ 平行
示例 S = S 2 ( r ) ⊂ R 3 S = S^2(r) \subset \mathbb R^3 S = S 2 ( r ) ⊂ R 3 γ ( t ) = ( r cos t r sin t 0 ) \boldsymbol \gamma(t) = \begin{pmatrix} r \cos t \\ r \sin t \\ 0 \end{pmatrix} γ ( t ) = ⎝ ⎛ r cos t r sin t 0 ⎠ ⎞ C ∞ C^\infty C ∞ f : R → R f: \mathbb R \to \mathbb R f : R → R
X ( t ) = γ ′ + ( 0 0 f ( t ) ) = ( − r sin t r cos t f ( t ) ) \boldsymbol X(t) = \boldsymbol \gamma' + \begin{pmatrix} 0 \\ 0 \\ f(t) \end{pmatrix} = \begin{pmatrix} -r \sin t \\ r \cos t \\ f(t) \end{pmatrix} X ( t ) = γ ′ + ⎝ ⎛ 0 0 f ( t ) ⎠ ⎞ = ⎝ ⎛ − r sin t r cos t f ( t ) ⎠ ⎞
沿曲线 γ \boldsymbol \gamma γ
证明 此时
X ( t ) ∈ T γ S = { ( ξ η ζ ) | ξ cos t + η sin t = 0 } \boldsymbol X(t) \in T_{\boldsymbol \gamma}S = \left\{\begin{pmatrix} \xi \\ \eta \\ \zeta \end{pmatrix} \middle| \xi \cos t + \eta \sin t = 0\right\} X ( t ) ∈ T γ S = ⎩ ⎪ ⎨ ⎪ ⎧ ⎝ ⎛ ξ η ζ ⎠ ⎞ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ξ cos t + η sin t = 0 ⎭ ⎪ ⎬ ⎪ ⎫
所以 X \boldsymbol X X γ \boldsymbol \gamma γ
D X d t ( t ) = ( 0 0 f ′ ( t ) ) \frac{D\boldsymbol X}{dt}(t) = \begin{pmatrix} 0 \\ 0 \\ f'(t) \end{pmatrix} d t D X ( t ) = ⎝ ⎛ 0 0 f ′ ( t ) ⎠ ⎞
得到
X 沿曲线 γ 平行 ⟺ f ( t ) 为常数 \boldsymbol X \text{ 沿曲线 } \boldsymbol \gamma \text{ 平行 } \iff f(t) \text{ 为常数} X 沿曲线 γ 平行 ⟺ f ( t ) 为常数
# 测地曲率以下令 ( S , n ) (S, \boldsymbol n) ( S , n ) S S S γ ( s ) \boldsymbol \gamma(s) γ ( s )
定义
κ g ( s ) = γ ′ ′ ( s ) tan \boldsymbol \kappa_g(s) = \boldsymbol \gamma''(s)_{\text{tan}} κ g ( s ) = γ ′ ′ ( s ) tan
为曲线 γ \boldsymbol \gamma γ ( S , n ) (S, \boldsymbol n) ( S , n ) 测地曲率向量 (geodesic curvature vector)「測地的曲率ベクトル」
κ n ( s ) = γ ′ ′ ( s ) nor \boldsymbol \kappa_n(s) = \boldsymbol \gamma''(s)_{\text{nor}} κ n ( s ) = γ ′ ′ ( s ) nor
为曲线 γ \boldsymbol \gamma γ ( S , n ) (S, \boldsymbol n) ( S , n ) 法曲率向量 (normal curvature vector)「法曲率ベクトル」
该两向量在各自管控的空间上的模长决定曲面在该方向上的弯曲程度,可以自然得到曲率
令 v = n ( γ ) × γ ′ \boldsymbol v = \boldsymbol n(\boldsymbol \gamma) \times \boldsymbol \gamma' v = n ( γ ) × γ ′ 标量函数 κ g ( s ) ∈ R \kappa_g(s) \in \mathbb R κ g ( s ) ∈ R
κ g ( s ) = κ g ( s ) v ( s ) \boldsymbol \kappa_g(s) = \kappa_g(s) \boldsymbol v(s) κ g ( s ) = κ g ( s ) v ( s )
此时称 κ g ( s ) \kappa_g(s) κ g ( s ) γ \boldsymbol \gamma γ ( S , n ) (S, \boldsymbol n) ( S , n ) 测地曲率 (geodesic curvature)「測地的曲率」
由于法曲率向量是法向量方向的分量,所以也唯一存在 标量函数 κ n ( s ) ∈ R \kappa_n(s) \in \mathbb R κ n ( s ) ∈ R
κ n ( s ) = κ n ( s ) n ( γ ( s ) ) \boldsymbol \kappa_n(s) = \kappa_n(s) \boldsymbol n(\boldsymbol \gamma(s)) κ n ( s ) = κ n ( s ) n ( γ ( s ) )
称 κ n ( s ) \kappa_n(s) κ n ( s ) γ \boldsymbol \gamma γ ( S , n ) (S, \boldsymbol n) ( S , n ) 法曲率 (normal curvature)「法曲率」
简要推导如下( γ ′ , v , n ( γ ) ) (\boldsymbol \gamma', \boldsymbol v, \boldsymbol n(\boldsymbol \gamma)) ( γ ′ , v , n ( γ ) ) R 3 \mathbb R^3 R 3
κ g ( s ) ∈ T γ ( s ) S ⟹ κ g ( s ) ⋅ n ( γ ( s ) ) = 0 \boldsymbol \kappa_g(s) \in T_{\boldsymbol \gamma(s)}S \implies \boldsymbol \kappa_g(s) \cdot \boldsymbol n(\boldsymbol \gamma(s)) = 0 κ g ( s ) ∈ T γ ( s ) S ⟹ κ g ( s ) ⋅ n ( γ ( s ) ) = 0
∥ γ ′ ( s ) ∥ = 1 ⟹ γ ′ ′ ( s ) ⋅ γ ′ ( s ) = 0 \|\boldsymbol \gamma'(s)\| = 1 \implies \boldsymbol \gamma''(s) \cdot \boldsymbol \gamma'(s) = 0 ∥ γ ′ ( s ) ∥ = 1 ⟹ γ ′ ′ ( s ) ⋅ γ ′ ( s ) = 0
κ g ( s ) ⋅ γ ′ ( s ) = ( γ ′ ′ ( s ) − κ n ( s ) ) ⋅ γ ′ ( s ) = γ ′ ′ ( s ) ⋅ γ ′ ( s ) − κ n ( s ) n ( γ ( s ) ) ⋅ γ ′ ( s ) ⏟ 0 = 0 \boldsymbol \kappa_g(s) \cdot \boldsymbol \gamma'(s) = (\boldsymbol \gamma''(s) - \boldsymbol \kappa_n(s)) \cdot \boldsymbol \gamma'(s) = \boldsymbol \gamma''(s) \cdot \boldsymbol \gamma'(s) - \kappa_n(s) \underbrace{\boldsymbol n(\boldsymbol \gamma(s)) \cdot \boldsymbol \gamma'(s)}_{0} = 0 κ g ( s ) ⋅ γ ′ ( s ) = ( γ ′ ′ ( s ) − κ n ( s ) ) ⋅ γ ′ ( s ) = γ ′ ′ ( s ) ⋅ γ ′ ( s ) − κ n ( s ) 0 n ( γ ( s ) ) ⋅ γ ′ ( s ) = 0
所以
κ g ( s ) = ( κ g ( s ) ⋅ γ ′ ( s ) ) ⏟ 第一分量 = 0 γ ′ ( s ) + ( κ g ( s ) ⋅ v ( s ) ) ⏟ 第二分量 v ( s ) + ( κ g ( s ) ⋅ n ( γ ( s ) ) ) ⏟ 第三分量 = 0 n ( γ ( s ) ) = ( κ g ( s ) ⋅ v ( s ) ) v ( s ) \boldsymbol \kappa_g(s) = \underbrace{(\boldsymbol \kappa_g(s) \cdot \boldsymbol \gamma'(s))}_{\text{第一分量}=0} \boldsymbol \gamma'(s) + \underbrace{(\boldsymbol \kappa_g(s) \cdot \boldsymbol v(s))}_{\text{第二分量}} \boldsymbol v(s) + \underbrace{(\boldsymbol \kappa_g(s) \cdot \boldsymbol n(\boldsymbol \gamma(s)))}_{\text{第三分量}=0} \boldsymbol n(\boldsymbol \gamma(s)) = (\boldsymbol \kappa_g(s) \cdot \boldsymbol v(s)) \boldsymbol v(s) κ g ( s ) = 第一分量 = 0 ( κ g ( s ) ⋅ γ ′ ( s ) ) γ ′ ( s ) + 第二分量 ( κ g ( s ) ⋅ v ( s ) ) v ( s ) + 第三分量 = 0 ( κ g ( s ) ⋅ n ( γ ( s ) ) ) n ( γ ( s ) ) = ( κ g ( s ) ⋅ v ( s ) ) v ( s )
所以存在唯一标量函数 κ g ( s ) \kappa_g(s) κ g ( s )
κ g ( s ) = κ g ( s ) v ( s ) \boldsymbol \kappa_g(s) = \kappa_g(s) \boldsymbol v(s) κ g ( s ) = κ g ( s ) v ( s )
若曲线非弧长参数化,即对于 γ ( t ) \boldsymbol \gamma(t) γ ( t )
s = ∫ t 0 t ∥ γ ′ ( τ ) ∥ d τ ⟹ d s d t = ∥ γ ′ ( t ) ∥ s = \int_{t_0}^t \|\boldsymbol \gamma'(\tau)\| d\tau \implies \frac{ds}{dt} = \|\boldsymbol \gamma'(t)\| s = ∫ t 0 t ∥ γ ′ ( τ ) ∥ d τ ⟹ d t d s = ∥ γ ′ ( t ) ∥
则
d 2 γ d s 2 ( s ) = 1 d s d t d d t ( 1 d s d t d γ d t ( t ) ) = 1 ∥ γ ′ ( t ) ∥ d d t ( 1 ∥ γ ′ ( t ) ∥ γ ′ ( t ) ) = γ ′ ′ ( t ) ∥ γ ′ ( t ) ∥ 2 − γ ′ ( t ) ∥ γ ′ ( t ) ∥ 4 ( γ ′ ( t ) ⋅ γ ′ ′ ( t ) ) \frac{d^2 \boldsymbol \gamma}{ds^2}(s) = \frac{1}{\frac{ds}{dt}} \frac{d}{dt} \left(\frac{1}{\frac{ds}{dt}} \frac{d\boldsymbol \gamma}{dt}(t)\right) = \frac{1}{\|\boldsymbol \gamma'(t)\|} \frac{d}{dt} \left(\frac{1}{\|\boldsymbol \gamma'(t)\|} \boldsymbol \gamma'(t)\right) = \frac{\boldsymbol \gamma''(t)}{\|\boldsymbol \gamma'(t)\|^2} - \frac{\boldsymbol \gamma'(t)}{\|\boldsymbol \gamma'(t)\|^4} \left(\boldsymbol \gamma'(t) \cdot \boldsymbol \gamma''(t)\right) d s 2 d 2 γ ( s ) = d t d s 1 d t d ( d t d s 1 d t d γ ( t ) ) = ∥ γ ′ ( t ) ∥ 1 d t d ( ∥ γ ′ ( t ) ∥ 1 γ ′ ( t ) ) = ∥ γ ′ ( t ) ∥ 2 γ ′ ′ ( t ) − ∥ γ ′ ( t ) ∥ 4 γ ′ ( t ) ( γ ′ ( t ) ⋅ γ ′ ′ ( t ) )
令 v ( t ) = n ( γ ( t ) ) × γ ′ ( t ) = 1 ∥ γ ′ ( t ) ∣ n ( γ ( t ) ) × γ ′ ( t ) \boldsymbol v(t) = \boldsymbol n(\boldsymbol \gamma(t)) \times \boldsymbol \gamma'(t) = \frac{1}{\|\boldsymbol \gamma'(t)|} \boldsymbol n(\boldsymbol \gamma(t)) \times \boldsymbol \gamma'(t) v ( t ) = n ( γ ( t ) ) × γ ′ ( t ) = ∥ γ ′ ( t ) ∣ 1 n ( γ ( t ) ) × γ ′ ( t )
则曲率
κ g = κ g ⋅ v = ( d 2 γ d s 2 − κ n ⏟ 与 n 平行 ) ⋅ v = d 2 γ d s 2 ⋅ v = 1 ∥ γ ′ ( t ) ∥ 2 d 2 γ d s 2 ⋅ ( n × γ ′ ) ⏟ 标量三重积 = 1 ∥ γ ′ ( t ) ∥ det ( d 2 γ d s 2 , n , γ ′ ) = 1 ∥ γ ′ ( t ) ∥ 3 det ( γ ′ , γ ′ ′ , n ) \begin{aligned} \kappa_g &= \boldsymbol \kappa_g \cdot \boldsymbol v \\ &= \left( \frac{d^2 \boldsymbol \gamma}{ds^2} - \underbrace{\boldsymbol \kappa_n}_{\text{与 } \boldsymbol n \text{ 平行}} \right) \cdot \boldsymbol v \\ &= \frac{d^2 \boldsymbol \gamma}{ds^2} \cdot \boldsymbol v \\ &= \frac{1}{\|\boldsymbol \gamma'(t)\|^2} \underbrace{\frac{d^2 \boldsymbol \gamma}{ds^2} \cdot (\boldsymbol n \times \boldsymbol \gamma')}_{\text{标量三重积}} \\ &= \frac{1}{\|\boldsymbol \gamma'(t)\|} \det(\frac{d^2 \boldsymbol \gamma}{ds^2}, \boldsymbol n, \boldsymbol \gamma') \\ &= \frac{1}{\|\boldsymbol \gamma'(t)\|^3} \det(\boldsymbol \gamma', \boldsymbol \gamma'', \boldsymbol n) \end{aligned} κ g = κ g ⋅ v = ⎝ ⎛ d s 2 d 2 γ − 与 n 平行 κ n ⎠ ⎞ ⋅ v = d s 2 d 2 γ ⋅ v = ∥ γ ′ ( t ) ∥ 2 1 标量三重积 d s 2 d 2 γ ⋅ ( n × γ ′ ) = ∥ γ ′ ( t ) ∥ 1 det ( d s 2 d 2 γ , n , γ ′ ) = ∥ γ ′ ( t ) ∥ 3 1 det ( γ ′ , γ ′ ′ , n )
即得结论,对于一般的曲线 γ ( t ) \boldsymbol \gamma(t) γ ( t )
κ g ( t ) = 1 ∥ γ ′ ( t ) ∥ 3 det ( γ ′ ( t ) , γ ′ ′ ( t ) , n ( γ ( t ) ) ) \kappa_g(t) = \frac{1}{\|\boldsymbol \gamma'(t)\|^3} \det(\boldsymbol \gamma'(t), \boldsymbol \gamma''(t), \boldsymbol n(\boldsymbol \gamma(t))) κ g ( t ) = ∥ γ ′ ( t ) ∥ 3 1 det ( γ ′ ( t ) , γ ′ ′ ( t ) , n ( γ ( t ) ) )
命题
曲线 γ \boldsymbol \gamma γ ∥ d γ d t ( t ) ∥ \|\frac{d\boldsymbol \gamma}{dt}(t)\| ∥ d t d γ ( t ) ∥ κ g ( t ) = 0 \kappa_g(t) = 0 κ g ( t ) = 0 ∀ t ∈ I \forall t \in I ∀ t ∈ I 证明 (1) ⟹ \implies ⟹
0 = γ ′ ′ ( t ) ⋅ γ ′ ( t ) = 1 2 d d t ( γ ′ ( t ) ⋅ γ ′ ( t ) ) = d d t ∥ γ ′ ( t ) ∥ 2 ⟹ ∥ γ ′ ( t ) ∥ 恒为常数 0 = \boldsymbol \gamma''(t) \cdot \boldsymbol \gamma'(t) = \frac{1}{2} \frac{d}{dt} (\boldsymbol \gamma'(t) \cdot \boldsymbol \gamma'(t)) = \frac{d}{dt} \|\boldsymbol \gamma'(t)\|^2 \implies \|\boldsymbol \gamma'(t)\| \text{ 恒为常数} 0 = γ ′ ′ ( t ) ⋅ γ ′ ( t ) = 2 1 d t d ( γ ′ ( t ) ⋅ γ ′ ( t ) ) = d t d ∥ γ ′ ( t ) ∥ 2 ⟹ ∥ γ ′ ( t ) ∥ 恒为常数
另一边
γ ′ ′ ( t ) ⊥ T γ ( t ) S ⟹ γ ′ ′ ( t ) = k ⋅ n ( γ ( t ) ) , k ∈ R ⟹ κ g ( t ) = 0 \boldsymbol \gamma''(t) \perp T_{\boldsymbol \gamma(t)}S \implies \boldsymbol \gamma''(t) = k \cdot \boldsymbol n(\boldsymbol \gamma(t)) ,\ k \in \mathbb R \implies \kappa_g(t) = 0 γ ′ ′ ( t ) ⊥ T γ ( t ) S ⟹ γ ′ ′ ( t ) = k ⋅ n ( γ ( t ) ) , k ∈ R ⟹ κ g ( t ) = 0
(2) ⟹ \implies ⟹ det ( γ ′ ( t ) , γ ′ ′ ( t ) , n ( γ ( t ) ) ) = 0 \det(\boldsymbol \gamma'(t), \boldsymbol \gamma''(t), \boldsymbol n(\boldsymbol \gamma(t))) = 0 det ( γ ′ ( t ) , γ ′ ′ ( t ) , n ( γ ( t ) ) ) = 0
γ ′ ′ ( t ) = a γ ′ ( t ) + b n ( γ ( t ) ) , a , b ∈ R \boldsymbol \gamma''(t) = a \boldsymbol \gamma'(t) + b \boldsymbol n(\boldsymbol \gamma(t)),\ a,b \in \mathbb R γ ′ ′ ( t ) = a γ ′ ( t ) + b n ( γ ( t ) ) , a , b ∈ R
γ ′ ( t ) ∈ T γ ( t ) S ⟹ γ ′ ( t ) ⋅ n ( γ ( t ) ) = 0 \boldsymbol \gamma'(t) \in T_{\boldsymbol \gamma(t)}S \implies \boldsymbol \gamma'(t) \cdot \boldsymbol n(\boldsymbol \gamma(t)) = 0 γ ′ ( t ) ∈ T γ ( t ) S ⟹ γ ′ ( t ) ⋅ n ( γ ( t ) ) = 0
所以
γ ′ ( t ) ⋅ γ ′ ′ ( t ) = a ∥ γ ′ ( t ) ∥ 2 \boldsymbol \gamma'(t) \cdot \boldsymbol \gamma''(t) = a \|\boldsymbol \gamma'(t)\|^2 γ ′ ( t ) ⋅ γ ′ ′ ( t ) = a ∥ γ ′ ( t ) ∥ 2
其中
γ ′ ( t ) ⋅ γ ′ ′ ( t ) = 1 2 d d t ∥ γ ′ ( t ) ∥ 2 = 0 ⟹ a = 0 \boldsymbol \gamma'(t) \cdot \boldsymbol \gamma''(t) = \frac{1}{2} \frac{d}{dt} \|\boldsymbol \gamma'(t)\|^2 = 0 \implies a = 0 γ ′ ( t ) ⋅ γ ′ ′ ( t ) = 2 1 d t d ∥ γ ′ ( t ) ∥ 2 = 0 ⟹ a = 0
所以
γ ′ ′ ( t ) = b n ( γ ( t ) ) ⊥ T γ ( t ) S \boldsymbol \gamma''(t) = b \boldsymbol n(\boldsymbol \gamma(t)) \perp T_{\boldsymbol \gamma(t)}S γ ′ ′ ( t ) = b n ( γ ( t ) ) ⊥ T γ ( t ) S
示例 S = S 2 ( r ) S = S^2(r) S = S 2 ( r ) n ( p ) = 1 r p , ∀ p ∈ S 2 ( r ) \boldsymbol n(\boldsymbol p) = \frac{1}{r} \boldsymbol p,\ \forall \boldsymbol p \in S^2(r) n ( p ) = r 1 p , ∀ p ∈ S 2 ( r ) ρ = r 2 − h 2 \rho = \sqrt{r^2 - h^2} ρ = r 2 − h 2 ∣ h ∣ < r |h| < r ∣ h ∣ < r
γ ( t ) = ( ρ cos t ρ sin t h ) , t ∈ R \boldsymbol \gamma(t) = \begin{pmatrix} \rho \cos t \\ \rho \sin t \\ h \end{pmatrix},\quad t \in \mathbb R γ ( t ) = ⎝ ⎛ ρ cos t ρ sin t h ⎠ ⎞ , t ∈ R
的测地曲率
解 γ ′ ( t ) = ( − ρ sin t ρ cos t 0 ) , γ ′ ′ ( t ) = ( − ρ cos t − ρ sin t 0 ) , n ( γ ( t ) ) = 1 r ( ρ cos t ρ sin t h ) \boldsymbol \gamma'(t) = \begin{pmatrix} -\rho \sin t \\ \rho \cos t \\ 0 \end{pmatrix},\quad \boldsymbol \gamma''(t) = \begin{pmatrix} -\rho \cos t \\ -\rho \sin t \\ 0 \end{pmatrix},\quad \boldsymbol n(\boldsymbol \gamma(t)) = \frac{1}{r} \begin{pmatrix} \rho \cos t \\ \rho \sin t \\ h \end{pmatrix} γ ′ ( t ) = ⎝ ⎛ − ρ sin t ρ cos t 0 ⎠ ⎞ , γ ′ ′ ( t ) = ⎝ ⎛ − ρ cos t − ρ sin t 0 ⎠ ⎞ , n ( γ ( t ) ) = r 1 ⎝ ⎛ ρ cos t ρ sin t h ⎠ ⎞
所以测地曲率
κ g ( t ) = 1 ∥ γ ′ ( t ) ∥ 3 det ( γ ′ ( t ) , γ ′ ′ ( t ) , n ( γ ( t ) ) ) = 1 r ρ 3 ∣ − ρ sin t − ρ cos t ρ cos t ρ cos t − ρ sin t ρ sin t 0 0 h ∣ = h r ρ \kappa_g(t) = \frac{1}{\|\boldsymbol \gamma'(t)\|^3} \det(\boldsymbol \gamma'(t), \boldsymbol \gamma''(t), \boldsymbol n(\boldsymbol \gamma(t))) = \frac{1}{r \rho^3} \begin{vmatrix} -\rho \sin t & -\rho \cos t & \rho \cos t \\ \rho \cos t & -\rho \sin t & \rho \sin t \\ 0 & 0 & h \end{vmatrix} = \frac{h}{r \rho} κ g ( t ) = ∥ γ ′ ( t ) ∥ 3 1 det ( γ ′ ( t ) , γ ′ ′ ( t ) , n ( γ ( t ) ) ) = r ρ 3 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ − ρ sin t ρ cos t 0 − ρ cos t − ρ sin t 0 ρ cos t ρ sin t h ∣ ∣ ∣ ∣ ∣ ∣ ∣ = r ρ h
# 最短路径令 ( S , n ) (S, \boldsymbol n) ( S , n ) S S S S S S p , q \boldsymbol p, \boldsymbol q p , q
问:在所有连接 p , q \boldsymbol p, \boldsymbol q p , q S S S
示例
平面上连接两点的最短路径为直线段 球面上连接两点的最短路径为大圆弧 最短路径的存在性并不能被直接保证,就算存在,也不保证唯一
示例
去心平面 S : = { z = 0 } ∖ { ( 0 0 0 ) } S := \{z = 0\} \setminus \{\left(\begin{smallmatrix}0\\0\\0\end{smallmatrix}\right)\} S : = { z = 0 } ∖ { ( 0 0 0 ) } p , − p ∈ S \boldsymbol p, -\boldsymbol p \in S p , − p ∈ S 球面 S = S 2 ( r ) S = S^2(r) S = S 2 ( r ) p = ( 0 0 r ) , q = ( 0 0 − r ) ∈ S \boldsymbol p = \left(\begin{smallmatrix}0\\0\\r\end{smallmatrix}\right),\ \boldsymbol q = \left(\begin{smallmatrix}0\\0\\-r\end{smallmatrix}\right) \in S p = ( 0 0 r ) , q = ( 0 0 − r ) ∈ S 令弧长参数化的曲线 x = γ ( s ) , s ∈ [ a , b ] \boldsymbol x = \boldsymbol \gamma(s),\ s \in [a,b] x = γ ( s ) , s ∈ [ a , b ]
起点与终点设定:γ ( a ) = p , γ ( b ) = q \boldsymbol \gamma(a) = \boldsymbol p,\ \boldsymbol \gamma(b) = \boldsymbol q γ ( a ) = p , γ ( b ) = q
以下给出变分法应用于几何对象上的定义
定义 S S S p , q ∈ S \boldsymbol p, \boldsymbol q \in S p , q ∈ S γ ( s ) : [ a , b ] → S \boldsymbol \gamma(s): [a,b] \to S γ ( s ) : [ a , b ] → S p , q \boldsymbol p, \boldsymbol q p , q C ∞ C^\infty C ∞ C ∞ C^\infty C ∞
F : ( − ϵ , ϵ ) × [ a , b ] → R 3 \boldsymbol F: (-\epsilon, \epsilon) \times [a,b] \to R^3 F : ( − ϵ , ϵ ) × [ a , b ] → R 3
满足
F ( λ , s ) ∈ S , ∀ ( λ , s ) ∈ ( − ϵ , ϵ ) × [ a , b ] \boldsymbol F(\lambda, s) \in S,\quad \forall (\lambda,s) \in (-\epsilon, \epsilon) \times [a,b] F ( λ , s ) ∈ S , ∀ ( λ , s ) ∈ ( − ϵ , ϵ ) × [ a , b ] F ( λ , a ) = p , F ( λ , b ) = q , ∀ λ ∈ ( − ϵ , ϵ ) \boldsymbol F(\lambda, a) = \boldsymbol p,\quad \boldsymbol F(\lambda, b) = \boldsymbol q,\quad \forall \lambda \in (-\epsilon, \epsilon) F ( λ , a ) = p , F ( λ , b ) = q , ∀ λ ∈ ( − ϵ , ϵ ) F ( 0 , s ) = γ ( s ) , ∀ s ∈ [ a , b ] \boldsymbol F(0,s) = \boldsymbol \gamma(s),\quad \forall s \in [a,b] F ( 0 , s ) = γ ( s ) , ∀ s ∈ [ a , b ] 则称 F \boldsymbol F F 以曲线 γ \boldsymbol \gamma γ 的一个 变分 (variation)「変分」
固定 λ \lambda λ γ λ ( s ) = F ( λ , s ) , s ∈ [ a , b ] \boldsymbol \gamma_\lambda(s) = \boldsymbol F(\lambda, s),\quad s \in [a,b] γ λ ( s ) = F ( λ , s ) , s ∈ [ a , b ] γ λ \boldsymbol \gamma_\lambda γ λ S S S p , q \boldsymbol p, \boldsymbol q p , q γ \boldsymbol \gamma γ 连续变形
并且,考虑对 λ \lambda λ
V F ( s ) : = ∂ F ∂ λ ( 0 , s ) V_{\boldsymbol F}(s) := \frac{\partial \boldsymbol F}{\partial \lambda}(0,s) V F ( s ) : = ∂ λ ∂ F ( 0 , s )
如果固定 s s s V F ( s ) V_{\boldsymbol F}(s) V F ( s ) S S S λ ↦ F ( λ , s ) \lambda \mapsto \boldsymbol F(\lambda,s) λ ↦ F ( λ , s ) λ = 0 \lambda = 0 λ = 0 λ \lambda λ γ \boldsymbol \gamma γ
V F ( s ) ∈ T γ ( s ) S , ∀ s ∈ [ a , b ] V_{\boldsymbol F}(s) \in T_{\boldsymbol \gamma(s)}S,\quad \forall s \in [a,b] V F ( s ) ∈ T γ ( s ) S , ∀ s ∈ [ a , b ]
通过变分分析,可以得出结论:最短路径的第一变分必须为零
命题 γ \boldsymbol \gamma γ p , q \boldsymbol p, \boldsymbol q p , q
∫ a b V F ( s ) ⋅ κ g ( s ) d s = 0 \int_a^b V_{\boldsymbol F}(s) \cdot \boldsymbol \kappa_g(s) ds = 0 ∫ a b V F ( s ) ⋅ κ g ( s ) d s = 0
证明 由 γ \boldsymbol \gamma γ F \boldsymbol F F γ λ \boldsymbol \gamma_\lambda γ λ
L ( λ ) = ∫ a b ∥ γ λ ′ ( s ) ∥ d s L(\lambda) = \int_a^b \left\|\boldsymbol \gamma_\lambda'(s)\right\| ds L ( λ ) = ∫ a b ∥ γ λ ′ ( s ) ∥ d s
在 λ = 0 \lambda = 0 λ = 0 γ λ ′ ( s ) = ∂ F ∂ s ( λ , s ) \boldsymbol \gamma_\lambda'(s) = \frac{\partial \boldsymbol F}{\partial s}(\lambda,s) γ λ ′ ( s ) = ∂ s ∂ F ( λ , s )
0 = d L d λ ( 0 ) = d d λ ∫ a b ∥ ∂ F ∂ s ( λ , s ) ∥ d s ∣ λ = 0 = d d λ ∫ a b ∂ F ∂ s ( λ , s ) ⋅ ∂ F ∂ s ( λ , s ) d s ∣ λ = 0 ⏟ Fundamental Theorem of Calculus = ∫ a b 1 2 ∥ ∂ F ∂ s ( 0 , s ) ∥ ⏟ = ∥ γ ′ ( s ) ∥ = 1 ∣ λ = 0 ⋅ d d λ ( ∂ F ∂ s ( λ , s ) ⋅ ∂ F ∂ s ( λ , s ) ) ∣ λ = 0 d s = ∫ a b ∂ 2 F ∂ λ ∂ s ( 0 , s ) ⋅ ∂ F ∂ s ( 0 , s ) ⏟ = γ ′ ( s ) d s = by parts [ ∂ F ∂ λ ( 0 , s ) ⋅ γ ′ ( s ) ] a b ⏟ = 0 − ∫ a b ∂ F ∂ λ ( 0 , s ) ⋅ γ ′ ′ ( s ) d s = − ∫ a b V F ( s ) ⋅ γ ′ ′ ( s ) d s \begin{aligned} 0 = \frac{dL}{d\lambda}(0) &= \frac{d}{d\lambda} \int_a^b \left\| \frac{\partial \boldsymbol F}{\partial s}(\lambda,s) \right\| ds \Bigg|_{\lambda=0} \\ &= \underbrace{\frac{d}{d\lambda} \int_a^b \sqrt{ \frac{\partial \boldsymbol F}{\partial s}(\lambda,s) \cdot \frac{\partial \boldsymbol F}{\partial s}(\lambda,s) } ds \Bigg|_{\lambda=0}}_{\text{Fundamental Theorem of Calculus}} \\ &= \int_a^b \frac{1}{2 \underbrace{\left\| \frac{\partial \boldsymbol F}{\partial s}(0,s) \right\|}_{= \|\boldsymbol \gamma'(s)\| = 1} \Bigg|_{\lambda=0}} \cdot \frac{d}{d\lambda} \left( \frac{\partial \boldsymbol F}{\partial s}(\lambda,s) \cdot \frac{\partial \boldsymbol F}{\partial s}(\lambda,s) \right) \Bigg|_{\lambda=0} ds \\ &= \int_a^b \frac{\partial^2 \boldsymbol F}{\partial \lambda \partial s}(0,s) \cdot \underbrace{\frac{\partial \boldsymbol F}{\partial s}(0,s)}_{= \boldsymbol \gamma'(s)} ds \\ &\stackrel{\text{by parts}}{=} \underbrace{\left[ \frac{\partial \boldsymbol F}{\partial \lambda}(0,s) \cdot \boldsymbol \gamma'(s) \right]_a^b}_{=0} - \int_a^b \frac{\partial \boldsymbol F}{\partial \lambda}(0,s) \cdot \boldsymbol \gamma''(s) ds \\ &= - \int_a^b V_{\boldsymbol F}(s) \cdot \boldsymbol \gamma''(s) ds \end{aligned} 0 = d λ d L ( 0 ) = d λ d ∫ a b ∥ ∥ ∥ ∥ ∥ ∂ s ∂ F ( λ , s ) ∥ ∥ ∥ ∥ ∥ d s ∣ ∣ ∣ ∣ ∣ ∣ λ = 0 = Fundamental Theorem of Calculus d λ d ∫ a b ∂ s ∂ F ( λ , s ) ⋅ ∂ s ∂ F ( λ , s ) d s ∣ ∣ ∣ ∣ ∣ ∣ λ = 0 = ∫ a b 2 = ∥ γ ′ ( s ) ∥ = 1 ∥ ∥ ∥ ∥ ∥ ∂ s ∂ F ( 0 , s ) ∥ ∥ ∥ ∥ ∥ ∣ ∣ ∣ ∣ ∣ ∣ λ = 0 1 ⋅ d λ d ( ∂ s ∂ F ( λ , s ) ⋅ ∂ s ∂ F ( λ , s ) ) ∣ ∣ ∣ ∣ ∣ ∣ λ = 0 d s = ∫ a b ∂ λ ∂ s ∂ 2 F ( 0 , s ) ⋅ = γ ′ ( s ) ∂ s ∂ F ( 0 , s ) d s = by parts = 0 [ ∂ λ ∂ F ( 0 , s ) ⋅ γ ′ ( s ) ] a b − ∫ a b ∂ λ ∂ F ( 0 , s ) ⋅ γ ′ ′ ( s ) d s = − ∫ a b V F ( s ) ⋅ γ ′ ′ ( s ) d s
由于 V F ( s ) ∈ T γ ( s ) S V_{\boldsymbol F}(s) \in T_{\boldsymbol \gamma(s)}S V F ( s ) ∈ T γ ( s ) S V F ( s ) ⋅ κ n ( s ) = 0 V_{\boldsymbol F}(s) \cdot \boldsymbol \kappa_n(s) = 0 V F ( s ) ⋅ κ n ( s ) = 0
V F ( s ) ⋅ γ ′ ′ ( s ) = V F ( s ) ⋅ ( κ g ( s ) + κ n ( s ) ) = V F ( s ) ⋅ κ g ( s ) V_{\boldsymbol F}(s) \cdot \boldsymbol \gamma''(s) = V_{\boldsymbol F}(s) \cdot \left( \boldsymbol \kappa_g(s) + \boldsymbol \kappa_n(s) \right) = V_{\boldsymbol F}(s) \cdot \boldsymbol \kappa_g(s) V F ( s ) ⋅ γ ′ ′ ( s ) = V F ( s ) ⋅ ( κ g ( s ) + κ n ( s ) ) = V F ( s ) ⋅ κ g ( s )
进一步得到
0 = − ∫ a b V F ( s ) ⋅ γ ′ ′ ( s ) d s = − ∫ a b V F ( s ) ⋅ κ g ( s ) d s 0 = - \int_a^b V_{\boldsymbol F}(s) \cdot \boldsymbol \gamma''(s) ds = - \int_a^b V_{\boldsymbol F}(s) \cdot \boldsymbol \kappa_g(s) ds 0 = − ∫ a b V F ( s ) ⋅ γ ′ ′ ( s ) d s = − ∫ a b V F ( s ) ⋅ κ g ( s ) d s
□ \square □
能否构造一个 “特别的变分” 使得变分的法向分量 V F ( s ) V_{\boldsymbol F}(s) V F ( s ) h ( s ) ⋅ κ g ( s ) h(s) \cdot \boldsymbol \kappa_g(s) h ( s ) ⋅ κ g ( s ) h ≥ 0 h \geq 0 h ≥ 0 0 0 0
命题 s 0 ∈ [ a , b ] s_0 \in [a,b] s 0 ∈ [ a , b ] γ \boldsymbol \gamma γ C ∞ C^\infty C ∞ h : [ a , b ] → R h:[a,b] \to \mathbb R h : [ a , b ] → R
V F ( s ) = h ( s ) ⋅ κ g ( s ) , ∀ s ∈ [ a , b ] V_{\boldsymbol F}(s) = h(s) \cdot \boldsymbol \kappa_g(s),\quad \forall s \in [a,b] V F ( s ) = h ( s ) ⋅ κ g ( s ) , ∀ s ∈ [ a , b ] h ( s ) ≥ 0 , h ( s 0 ) > 0 h(s) \geq 0,\ h(s_0) \gt 0 h ( s ) ≥ 0 , h ( s 0 ) > 0 证明 取 γ \boldsymbol \gamma γ σ : D → R 3 \boldsymbol \sigma: D \to \mathbb R^3 σ : D → R 3 γ ( s ) ∈ σ ( D ) \boldsymbol \gamma(s) \in \boldsymbol \sigma(D) γ ( s ) ∈ σ ( D ) s s s γ ( s ) = σ ( u 1 ( s ) , u 2 ( s ) ) \boldsymbol \gamma(s) = \boldsymbol \sigma(u^1(s), u^2(s)) γ ( s ) = σ ( u 1 ( s ) , u 2 ( s ) )
κ g ( s ) = κ g 1 ( s ) σ 1 ( u 1 ( s ) , u 2 ( s ) ) + κ g 2 ( s ) σ 2 ( u 1 ( s ) , u 2 ( s ) ) \boldsymbol \kappa_g(s) = \kappa_g^1(s) \boldsymbol \sigma_1(u^1(s), u^2(s)) + \kappa_g^2(s) \boldsymbol \sigma_2(u^1(s), u^2(s)) κ g ( s ) = κ g 1 ( s ) σ 1 ( u 1 ( s ) , u 2 ( s ) ) + κ g 2 ( s ) σ 2 ( u 1 ( s ) , u 2 ( s ) )
取极小半径与误差 ρ , ϵ > 0 \rho, \epsilon \gt 0 ρ , ϵ > 0
∣ s − s 0 ∣ < ρ , ∣ λ ∣ < ϵ ⟹ ( u 1 ( s ) + λ κ g 1 ( s ) u 2 ( s ) + λ κ g 2 ( s ) ) ∈ D |s - s_0| \lt \rho, \ |\lambda| \lt \epsilon \implies \begin{pmatrix} u^1(s) + \lambda \kappa_g^1(s) \\[4pt] u^2(s) + \lambda \kappa_g^2(s) \end{pmatrix} \in D ∣ s − s 0 ∣ < ρ , ∣ λ ∣ < ϵ ⟹ ( u 1 ( s ) + λ κ g 1 ( s ) u 2 ( s ) + λ κ g 2 ( s ) ) ∈ D
通过 ρ , ϵ \rho, \epsilon ρ , ϵ
h ( s ) = { exp ( − 1 ρ 2 − ( s − s 0 ) 2 ) , ∣ s − s 0 ∣ < ρ 0 , otherwise h(s) = \begin{cases} \exp\left( -\frac{1}{\rho^2 - (s - s_0)^2} \right), & |s - s_0| \lt \rho \\ 0, & \text{otherwise} \end{cases} h ( s ) = { exp ( − ρ 2 − ( s − s 0 ) 2 1 ) , 0 , ∣ s − s 0 ∣ < ρ otherwise
F ( λ , s ) = { σ ( u 1 ( s ) + λ h ( s ) κ g 1 ( s ) , u 2 ( s ) + λ h ( s ) κ g 2 ( s ) ) , ∣ s − s 0 ∣ < ρ , ∣ λ ∣ < ϵ γ ( s ) , otherwise F(\lambda, s) = \begin{cases} \boldsymbol \sigma\left( u^1(s) + \lambda h(s) \kappa_g^1(s),\ u^2(s) + \lambda h(s) \kappa_g^2(s) \right), & |s - s_0| \lt \rho,\ |\lambda| \lt \epsilon \\ \boldsymbol \gamma(s), & \text{otherwise} \end{cases} F ( λ , s ) = { σ ( u 1 ( s ) + λ h ( s ) κ g 1 ( s ) , u 2 ( s ) + λ h ( s ) κ g 2 ( s ) ) , γ ( s ) , ∣ s − s 0 ∣ < ρ , ∣ λ ∣ < ϵ otherwise
则 F \boldsymbol F F γ \boldsymbol \gamma γ
V F ( s ) = ∂ F ∂ λ ( 0 , s ) = h ( s ) ( κ g 1 ( s ) σ 1 ( u 1 ( s ) , u 2 ( s ) ) + κ g 2 ( s ) σ 2 ( u 1 ( s ) , u 2 ( s ) ) ) = h ( s ) ⋅ κ g ( s ) V_{\boldsymbol F}(s) = \frac{\partial \boldsymbol F}{\partial \lambda}(0,s) = h(s) \left( \kappa_g^1(s) \boldsymbol \sigma_1(u^1(s), u^2(s)) + \kappa_g^2(s) \boldsymbol \sigma_2(u^1(s), u^2(s)) \right) = h(s) \cdot \boldsymbol \kappa_g(s) V F ( s ) = ∂ λ ∂ F ( 0 , s ) = h ( s ) ( κ g 1 ( s ) σ 1 ( u 1 ( s ) , u 2 ( s ) ) + κ g 2 ( s ) σ 2 ( u 1 ( s ) , u 2 ( s ) ) ) = h ( s ) ⋅ κ g ( s )
□ \square □
从此命题可以证明一个重要结论,测地线为连接两点的最短路径的必要条件
定理 γ \boldsymbol \gamma γ p , q \boldsymbol p, \boldsymbol q p , q γ \boldsymbol \gamma γ
证明 根据最短路径条件,可得
∫ a b V F ( s ) ⋅ κ g ( s ) d s = 0 \int_a^b V_{\boldsymbol F}(s) \cdot \boldsymbol \kappa_g(s) ds = 0 ∫ a b V F ( s ) ⋅ κ g ( s ) d s = 0
应用前一命题中构造的变分存在性,可以得到
∫ a b V F ( s ) ⋅ κ g ( s ) d s = ∫ a b ( h ( s ) ⋅ κ g ( s ) ) ⋅ κ g ( s ) d s = ∫ a b h ( s ) ∥ κ g ( s ) ∥ 2 d s = 0 \int_a^b V_{\boldsymbol F}(s) \cdot \boldsymbol \kappa_g(s) ds = \int_a^b (h(s) \cdot \boldsymbol \kappa_g(s)) \cdot \boldsymbol \kappa_g(s) ds = \int_a^b h(s) \|\boldsymbol \kappa_g(s)\|^2 ds = 0 ∫ a b V F ( s ) ⋅ κ g ( s ) d s = ∫ a b ( h ( s ) ⋅ κ g ( s ) ) ⋅ κ g ( s ) d s = ∫ a b h ( s ) ∥ κ g ( s ) ∥ 2 d s = 0
由于 h ( s ) ≥ 0 h(s) \geq 0 h ( s ) ≥ 0 0 0 0
∥ κ g ( s ) ∥ 2 = 0 , ∀ s ∈ [ a , b ] \|\boldsymbol \kappa_g(s)\|^2 = 0,\quad \forall s \in [a,b] ∥ κ g ( s ) ∥ 2 = 0 , ∀ s ∈ [ a , b ]
即 κ g ≡ 0 \boldsymbol \kappa_g \equiv \boldsymbol 0 κ g ≡ 0 γ \boldsymbol \gamma γ ∥ γ ′ ( s ) ∥ \|\boldsymbol \gamma'(s)\| ∥ γ ′ ( s ) ∥ □ \square □