# 集合族

许多情况下我们需要讨论多个集合而不是单个集合。为了整理和标记这些集合，需要一个添字集

令 $\Lambda$ 为一个非空集合，通过将 $\Lambda$ 中的每一个元素 $\lambda \in \Lambda$ 都映射到一个集合 $A_\lambda$ ，那么 $\Lambda$ 成为 添字集 (index set)「添字集合」
此时映射得到的全体集合，称为被添字集 $\Lambda$ 所添的 集合族 (family of sets)「集合族」，记为 $\{ A_\lambda \}_{\lambda \in \Lambda}$
注意基于映射的性质，即使 $\Lambda$ 中所有的元都映射到同一个集合，那么它仍然可以成为一个集合族

如同集合之间的相等要求的是完全对齐，集合族的相等要求更加严格，对于两个不同的集合族，首先它们的添字集必须相等，其次需要满足

$\{A_\lambda\}_{\lambda \in \Lambda} = \{B_\lambda\}_{\lambda \in \Lambda} \iff {}^\forall \lambda \in \Lambda: A_\lambda = B_\lambda$

示例

设 $\mathbb N_{\leq n} := \{1, 2, \ldots, n\}$ ，则 $\{ \mathbb N_{\leq n} \}_{n \in \mathbb N}$ 是一个以 $\mathbb N$ 为添字集的集合族，一般地以 $\mathbb N$ 为添字集的集合族称为集合列
记球面 $S^2(r) := \{(x, y, z) \in \mathbb R^3 \mid x^2 + y^2 + z^2 = r^2\}$ ，则 $\{ S^2(r) \}_{r \in \mathbb R_{>0}}$ 是一个以正实数集为添字集的集合族

令 $X$ 为一个集合，称集合族 $\{A_\lambda\}_{\lambda \in \Lambda}$ 为 $X$ 的 子集族 (family of subsets)「部分集合族」，当且仅当

${}^\forall \lambda \in \Lambda: A_\lambda \subset X$

# 集合族的交并运算

定义
令 $\{A_\lambda\}_{\lambda \in \Lambda}$ 为以 $\Lambda$ 为添字集的集合族，定义 $\{A_\lambda\}_{\lambda \in \Lambda}$ 的 并集 (Union)「和集合」 为

$\bigcup_{\lambda \in \Lambda} A_\lambda := \{ x \mid {}^\exists \lambda \in \Lambda: x \in A_\lambda \}$

定义 $\{A_\lambda\}_{\lambda \in \Lambda}$ 的 交集 (Intersection)「共通集合」 为

$\bigcap_{\lambda \in \Lambda} A_\lambda := \{ x \mid {}^\forall \lambda \in \Lambda: x \in A_\lambda \}$

集合族的交并运算极度重要且常用，如果不熟练，会导致后续的点集拓扑学习有巨大困难，所以需要多多练习并理解本质

简单来说

集合族的并集是，将所有集合里的所有元全部列举出来
集合族的交集是，只保留所有集合中都包含的全部共通的元

如果 $\Lambda = \{1, 2, \ldots, n\}$ 是一个有限集合，那么交并运算也可以写作

$\bigcup_{\lambda \in \Lambda} A_\lambda = \bigcup_{i=1}^n A_i = A_1 \cup A_2 \cup \cdots \cup A_n$

$\bigcap_{\lambda \in \Lambda} A_\lambda = \bigcap_{i=1}^n A_i = A_1 \cap A_2 \cap \cdots \cap A_n$

提醒：不要默认所有的添字集都是有限的

如果 $\{A_\lambda\}_{\lambda \in \Lambda}$ 是 $X$ 的子集族，那么显然有

$\bigcup_{\lambda \in \Lambda} A_\lambda \subset X, \quad \bigcap_{\lambda \in \Lambda} A_\lambda \subset X$

请参考以下练习示例。通常来说问题的原型是 “求出集合族的交并集”，但在实际问题中，解决的方法往往是通过类似直觉或者图画来找到规律，并给出一个猜测的答案，再去证明运算结果等于这个答案

示例

\displaystyle\bigcup_{r \in (0, +\infty)} S^2(r) = \mathbb R^3 \setminus \
$\displaystyle\bigcup_{n \in \mathbb N} (-\frac{1}{n}, n] = (-1, +\infty)$
$\displaystyle\bigcap_{n \in \mathbb N} (-\frac{1}{n}, n] = [0,1]$

证明

(1)
( $\subseteq$ )
取 $(x,y,z) \in \displaystyle\bigcup_{r \in (0, +\infty)} S^2(r)$ ，则

${}^\exists r_0 \in (0, +\infty): (x,y,z) \in S^2(r_0) \implies x^2 + y^2 + z^2 = r_0^2 > 0 \implies (x,y,z) \neq (0,0,0)$

因此 (x,y,z) \in \mathbb R^3 \setminus \

( $\supseteq$ )
取 $(x,y,z) \in \mathbb R^3 \setminus \{(0,0,0)\}$ ，令

$r = \sqrt{x^2 + y^2 + z^2}$

显然 $r \gt 0$ ，且 $(x,y,z) \in S^2(r)$ ，因此 $(x,y,z) \in \displaystyle\bigcup_{r \in (0, +\infty)} S^2(r)$

(2)
( $\subseteq$ )
取 $x \in \displaystyle\bigcup_{n \in \mathbb N} (-\frac{1}{n}, n]$ ，则

${}^\exists n_0 \in \mathbb N: x \in (-\frac{1}{n_0}, n_0] \implies -\frac{1}{n_0} < x \leq n_0$

由于 $-\frac{1}{n_0} \gt -1$ 且 $n_0 \geq 1$ ，因此 $-1 < x \leq n_0$ ，即 $x \in (-1, +\infty)$

( $\supseteq$ )
取 $x \in (-1, +\infty)$

如果 $x \geq 0$ ，那么只需要找一个大于 $x$ 的自然数 $n_0$ ，则 $x \in (-\frac{1}{n_0}, n_0]$
如果 $-1 \lt x \lt 0$ ，那么显然 $x \in (-1, 0) \subset (-\frac{1}{1}, 1]$

因此 $x \in \displaystyle\bigcup_{n \in \mathbb N} (-\frac{1}{n}, n]$

(3)
( $\subseteq$ )
取 $x \in \displaystyle\bigcap_{n \in \mathbb N} (-\frac{1}{n}, n]$ ，则

${}^\forall n \in \mathbb N: x \in (-\frac{1}{n}, n] \implies {}^\forall n \in \mathbb N: -\frac{1}{n} < x \leq n$

由于 $\displaystyle\lim_{n \to +\infty} -\frac{1}{n} = 0$ ，因此 $x \geq 0$ ，且由于对任意 $n$ 都有 $x \leq n$ ，因此 $x \leq 1$ ，即 $x \in [0,1]$

( $\supseteq$ )
取 $x \in [0,1]$ ，则对于任意 $n \in \mathbb N$ ，都有

$-\frac{1}{n} < 0 \leq x \leq 1 \leq n$

因此 $x \in (-\frac{1}{n}, n]$ ，即 $x \in \displaystyle\bigcap_{n \in \mathbb N} (-\frac{1}{n}, n]$
$\square$

集合族的交并运算也可以实现 De Morgan 律

定理 集合族的 De Morgan 律
令 $\{A_\lambda\}_{\lambda \in \Lambda}$ 为 $X$ 的子集族，则有

$\displaystyle\left( \bigcup_{\lambda \in \Lambda} A_\lambda \right)^c = \bigcap_{\lambda \in \Lambda} A_\lambda^c$
$\displaystyle\left( \bigcap_{\lambda \in \Lambda} A_\lambda \right)^c = \bigcup_{\lambda \in \Lambda} A_\lambda^c$

证明

(1)
根据定义

$\begin{aligned} \left( \bigcup_{\lambda \in \Lambda} A_\lambda \right)^c &= \{ x \in X \mid x \not\in \bigcup_{\lambda \in \Lambda} A_\lambda \} \\ &= \{ x \in X \mid {}^\forall \lambda \in \Lambda: x \not\in A_\lambda \} \\ &= \{ x \in X \mid {}^\forall \lambda \in \Lambda: x \in A_\lambda^c \} \\ &= \bigcap_{\lambda \in \Lambda} A_\lambda^c \end{aligned}$

(2)
令 $B_\lambda := A_\lambda^c$ ，则根据 (1) 有

$\left( \bigcup_{\lambda \in \Lambda} B_\lambda \right)^c = \bigcap_{\lambda \in \Lambda} B_\lambda^c$

所以

$\left( \bigcap_{\lambda \in \Lambda} A_\lambda^c \right)^c = \bigcup_{\lambda \in \Lambda} (A_\lambda^c)^c = \bigcup_{\lambda \in \Lambda} A_\lambda$

取补集得

$\left( \bigcap_{\lambda \in \Lambda} A_\lambda \right)^c = \bigcup_{\lambda \in \Lambda} A_\lambda^c$

$\square$

映射的像与原象也可以得到推广

命题
令映射 $f: X \to Y$ ，以及 $X$ 的子集族 $\{A_\lambda\}_{\lambda \in \Lambda}$ 和 $Y$ 的子集族 $\{B_\mu\}_{\mu \in M}$ ，则有

$\displaystyle f\left( \bigcup_{\lambda \in \Lambda} A_\lambda \right) = \bigcup_{\lambda \in \Lambda} f(A_\lambda)$
$\displaystyle f\left( \bigcap_{\lambda \in \Lambda} A_\lambda \right) \subseteq \bigcap_{\lambda \in \Lambda} f(A_\lambda)$
$\displaystyle f^{-1}\left( \bigcup_{\mu \in M} B_\mu \right) = \bigcup_{\mu \in M} f^{-1}(B_\mu)$
$\displaystyle f^{-1}\left( \bigcap_{\mu \in M} B_\mu \right) = \bigcap_{\mu \in M} f^{-1}(B_\mu)$

证明

(1)
( $\subseteq$ )
取 $y \in f\left( \bigcup_{\lambda \in \Lambda} A_\lambda \right)$ ，则

${}^\exists x \in \bigcup_{\lambda \in \Lambda} A_\lambda: f(x) = y$

因此存在某个 $\lambda_0 \in \Lambda$ ，使得 $x \in A_{\lambda_0}$ ，所以 $y = f(x) \in f(A_{\lambda_0}) \subseteq \bigcup_{\lambda \in \Lambda} f(A_\lambda)$

( $\supseteq$ )
取 $y \in \bigcup_{\lambda \in \Lambda} f(A_\lambda)$ ，则存在某个 $\lambda_0 \in \Lambda$ ，使得

$y \in f(A_{\lambda_0}) \implies {}^\exists x \in A_{\lambda_0}: f(x) = y$

因此 $x \in \bigcup_{\lambda \in \Lambda} A_\lambda$ ，所以 $y \in f\left( \bigcup_{\lambda \in \Lambda} A_\lambda \right)$

(2)
取 $y \in f\left( \bigcap_{\lambda \in \Lambda} A_\lambda \right)$ ，则

${}^\exists x \in \bigcap_{\lambda \in \Lambda} A_\lambda: f(x) = y$

因此对于任意 $\lambda \in \Lambda$ ，都有 $x \in A_\lambda$ ，所以 $y = f(x) \in f(A_\lambda)$ ，即 $y \in \bigcap_{\lambda \in \Lambda} f(A_\lambda)$

(3)
根据定义

$\begin{aligned} f^{-1}\left( \bigcup_{\mu \in M} B_\mu \right) &= \{ x \in X \mid f(x) \in \bigcup_{\mu \in M} B_\mu \} \\ &= \{ x \in X \mid {}^\exists \mu \in M: f(x) \in B_\mu \} \\ &= \bigcup_{\mu \in M} \{ x \in X \mid f(x) \in B_\mu \} \\ &= \bigcup_{\mu \in M} f^{-1}(B_\mu) \end{aligned}$

(4)
根据定义

$\begin{aligned} f^{-1}\left( \bigcap_{\mu \in M} B_\mu \right) &= \{ x \in X \mid f(x) \in \bigcap_{\mu \in M} B_\mu \} \\ &= \{ x \in X \mid {}^\forall \mu \in M: f(x) \in B_\mu \} \\ &= \bigcap_{\mu \in M} \{ x \in X \mid f(x) \in B_\mu \} \\ &= \bigcap_{\mu \in M} f^{-1}(B_\mu) \end{aligned}$

$\square$

# 直和与直积

在考虑直和前，让我们先引入非交并

定义
令集合 $X$ 和其子集族 $\{A_\lambda\}_{\lambda \in \Lambda}$ ，称 $\{A_\lambda\}_{\lambda \in \Lambda}$ 为 $X$ 的 非交并 (Disjoint Union)「非交和」，当且仅当

$X = \bigcup_{\lambda \in \Lambda} A_\lambda$
$\lambda,\mu \in \Lambda, \lambda \neq \mu \implies A_\lambda \cap A_\mu = \emptyset$

此时记作

$X = \bigsqcup_{\lambda \in \Lambda} A_\lambda$

简单来说，各个集合之间不存在交集

有限个非交并往往也写作类似 $A \sqcup B \sqcup C$ 这样的形式

注意，以 $X$ 作为全集的集合 $A,B$ 满足

$B = A^c \iff X = A \sqcup B \iff X = A \cup B \text{ and } A \cap B = \emptyset$

示例

$\mathbb R = \displaystyle\bigsqcup_{n \in \mathbb Z} [n, n+1)$
$\mathbb R^3 \setminus \{(0,0,0)\} = \displaystyle\bigsqcup_{r \in (0, +\infty)} S^2(r)$

非交并的定义具有以下等价表述

命题
令集合 $X$ 和其子集族 $\{A_\lambda\}_{\lambda \in \Lambda}$ ，则以下命题等价

$X$ 是 $\{A_\lambda\}_{\lambda \in \Lambda}$ 的非交并
对于任意 $x \in X$ ，存在且仅存在一个 $\lambda_0 \in \Lambda$ ，使得 x \in A_

证明

( $\Rightarrow$ )
取 $x \in X$ ，根据条件有

${}^\exists \lambda \in \Lambda: x \in A_\lambda$

如果存在 $\mu \in \Lambda, \mu \neq \lambda$ ，使得

$x \in A_\mu$

那么 $x \in A_\lambda \cap A_\mu$ ，与条件矛盾，因此该 $\lambda$ 是唯一的

( $\Leftarrow$ )
取任意 $x \in X$ ，根据条件有

${}^\exists! \lambda \in \Lambda: x \in A_\lambda$

因此 $x \in \bigcup_{\lambda \in \Lambda} A_\lambda$ ，所以

$X \subseteq \bigcup_{\lambda \in \Lambda} A_\lambda$

另一边，子集族给出了反向包含关系，所以

$X = \bigcup_{\lambda \in \Lambda} A_\lambda$

进一步，取 $\lambda, \mu \in \Lambda, \lambda \neq \mu$ ，如果存在 $x \in A_\lambda \cap A_\mu$ ，那么 $x$ 同时属于 $A_\lambda$ 和 $A_\mu$ ，与条件矛盾，因此

$A_\lambda \cap A_\mu = \emptyset$

$\square$

定义
集合族 $\{A_\lambda\}_{\lambda \in \Lambda}$ 的 直和 (Direct Sum)「直和」，定义为

$\coprod_{\lambda \in \Lambda} A_\lambda := \left\{ (x, \lambda) \mid \lambda \in \Lambda, x \in A_\lambda \right\}$

如果对各个 $\lambda$ ，令

$A_\lambda^* := \{\lambda\} \times A_\lambda = \{(\lambda, x) \mid x \in A_\lambda\}$

那么直和可以写作

$\coprod_{\lambda \in \Lambda} A_\lambda = \bigsqcup_{\lambda \in \Lambda} A_\lambda^*$

一般来说集合族的并不一定是非交并，但是通过对每一个集合赋予一个 $\lambda$ 标签，这使得新的集合 $A_\lambda^*$ 成为一个更高维度上的切片，即使各个集合之间存在交集，但是因为在切片的位置不同，所以直和一定是非交并诞生的

一个较为直观的例子是，三维空间中运动的物体，在四维时空中看来，它将以一个 “残影” 的形式存在，不同时间点下不为之可能相同，也可能不同，但是一定能完整撑起整个四维结构

示例
考虑以下集合族：令 $\lambda \in [0,1]$

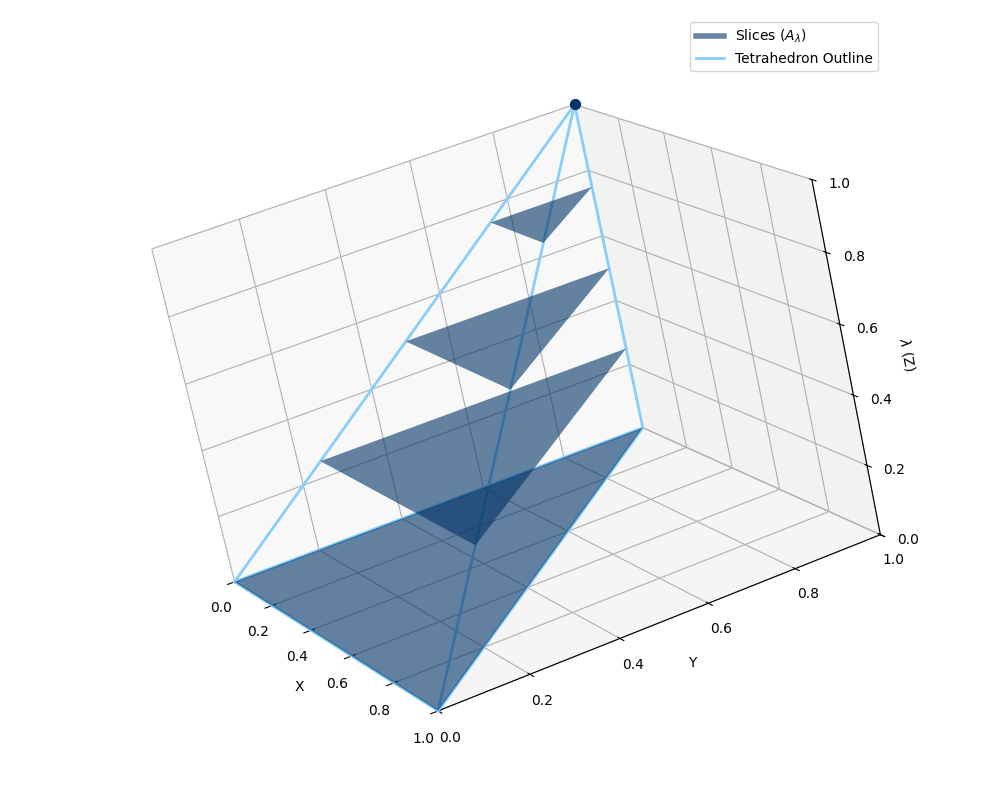
$A_\lambda := \{(x,y) \in \mathbb R^2 \mid x \geq 0, y \geq \lambda, x + y \leq 1\}$

则其切片与集合如图所示

展开查看

数学中常用连乘符号表示多个乘积，例如对于 $n$ 个集合的直积，可以写作

$\prod_{i=1}^n A_i := A_1 \times A_2 \times \cdots \times A_n$

实际上，直积可以看作是一般的映射。令

$A := \prod_{i=1}^n A_i$

那么对于 $A$ 中的任意元 $(a_1, a_2, \ldots, a_n)$ ，各个成分都属于 $A$ ，所以可以定义映射

$a:\{1,2,\ldots,n\} \to \bigcup_{i=1}^n A_i = A$

这样一来， $a(i) \in A_i$ ，因此 $A$ 中的元可以看作是从添字集 $\{1,2,\ldots,n\}$ 到各个集合 $A_i$ 的映射
也就是说，以下两种描述是等价的

直积中的元 $(a_1, a_2, \ldots, a_n)$
由 $\{1,2,\ldots,n\}$ 到 $\bigcup_{i=1}^n A_i$ 的映射 $i \mapsto a_i$

因此，我们得到直积的一般定义

定义
令集合族 $\{A_\lambda\}_{\lambda \in \Lambda}$ ，其 直积 (Direct Product)「直积」 定义为

$\prod_{\lambda \in \Lambda} A_\lambda := \left\{ a: \Lambda \to \bigcup_{\lambda \in \Lambda} A_\lambda \mid {}^\forall \lambda \in \Lambda: a(\lambda) \in A_\lambda \right\}$

对于各个直积中的元，其映射值 $a(\lambda)$ 称为该元在 $\lambda$ 处的 分量 (component)「成分」，记为 $a_\lambda := a(\lambda)$

对于各个记号 $\lambda \in \Lambda$ ，定义映射

$\mathrm{pr}_\lambda: \prod_{\mu \in \Lambda} A_\mu \to A_\lambda$

称为在 $\lambda$ 处的 投影 (projection)「射影」

如果 $A_\lambda$ 全都是同一个集合 $A$ ，那么由于 $\bigcup_{\lambda \in \Lambda} A_\lambda = A$ ，所以直积可以简化为

$\prod_{\lambda \in \Lambda} A_\lambda = \left\{ a: \Lambda \to A \right\}$

也就是说，直积将会表示为从添字集 $\Lambda$ 到集合 $A$ 的所有映射的集合
一般地，由 $\Lambda$ 到 $A$ 的映射集合记为 $A^\Lambda$

示例

在等价表述的考虑下 $X^{\{1,2,\ldots,n\}} = X^n$ ，即 $n$ - 元组的集合
$\mathbb R^{\mathbb N}$ 表示所有实数列的集合

从直积出发，可以得到一个非常著名，也充满争议的公理

公理 选择公理 (Axiom of Choice)
令 $\Lambda$ 非空
若对于任意 $\lambda \in \Lambda$ ，都有非空集合 $A_\lambda$ ，则直积 $\displaystyle\prod_{\lambda \in \Lambda} A_\lambda$ 非空

选择公理的正确性实际上并不能得到保证，但是目前广泛接受其作为一般事实

基于选择公理可以得到以下结论

命题
令 $X,Y$ 为非空集合，则对于任意满射的映射 $f: X \to Y$ ，都存在映射 $g: Y \to X$ ，使得

$f \circ g = \mathrm{id}_Y$

证明

对于各个 $y \in Y$ ，令

$X_y := f^{-1}(\{y\}) = \{ x \in X \mid f(x) = y \}$

由于 $f$ 是满射，所以对于任意 $y \in Y$ ，都有 $X_y \neq \emptyset$ 。因此根据选择公理，直积

$\prod_{y \in Y} X_y$

非空，取 $g \in \displaystyle\prod_{y \in Y} X_y$ ，则对于任意 $y \in Y$ ，都有 $g(y) \in X_y$ ，所以

$f(g(y)) = y$

因此 $f \circ g = \mathrm{id}_Y$
$\square$

实际上，如果默认上述命题成立，也可以反向导出选择公理，因此二者在逻辑上是等价的

# 集合族

# 集合族的交并运算

# 直和与直积

【集合论】4-等价关系

【集合论】1-集合