对于在微分几何中常见的数种曲面进行介绍与计算
以下 $S = f(\{0\}),\quad \boldsymbol \sigma: D \to S$
曲率计算仅考虑 $\boldsymbol \sigma(D)$

计算包含项目

• 曲面方程与参数表示
• 正向法向量场
• 第一基本形式
• 第二基本形式
• 曲率

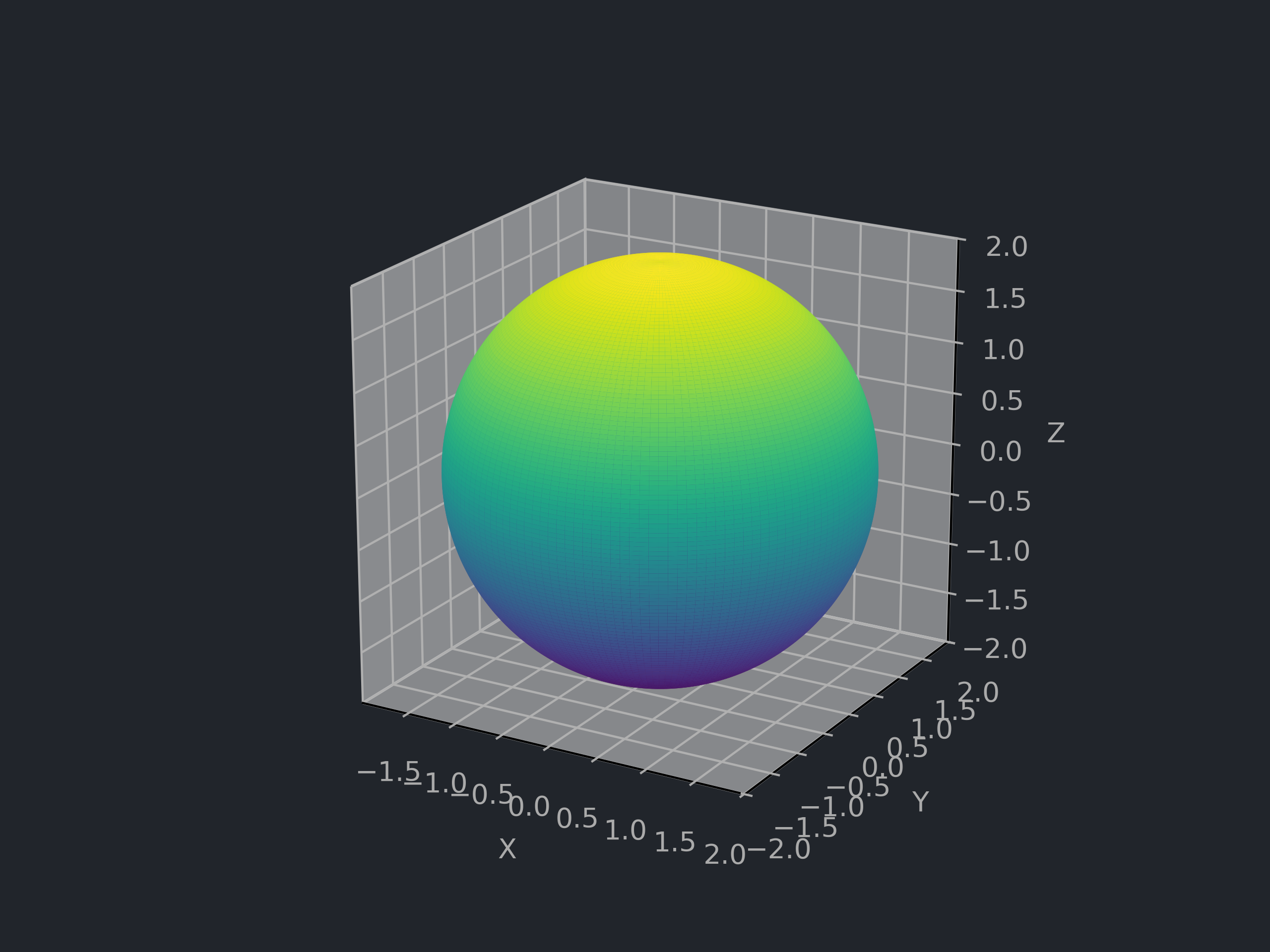
# 球面 Sphere

# 曲面方程与参数表示

$r > 0,\quad D = (0,\pi) \times (0,2\pi)$

$$f(x,y,z) = x^2 + y^2 + z^2 - r^2,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} r \sin u \cos v \\ r \sin u \sin v \\ r \cos u \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} r \cos u \cos v \\ r \cos u \sin v \\ -r \sin u \end{pmatrix} \times \begin{pmatrix} -r \sin u \sin v \\ r \sin u \cos v \\ 0 \end{pmatrix} = \begin{pmatrix} r^2 \sin^2 u \cos v \\ r^2 \sin^2 u \sin v \\ r^2 \sin u \cos u \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \begin{pmatrix} \sin u \cos v \\ \sin u \sin v \\ \cos u \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = r^2$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = 0,$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = r^2 \sin^2 u$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \begin{pmatrix} -r \sin u \cos v \\ -r \sin u \sin v \\ -r \cos u \end{pmatrix},\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} -r \cos u \sin v \\ r \cos u \cos v \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} -r \sin u \cos v \\ -r \sin u \sin v \\ 0 \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = -r$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = -r \sin^2 u$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{1}{r^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = -\frac{1}{r}$$

$$\kappa_1 = -\frac{1}{r},\quad \kappa_2 = -\frac{1}{r}$$

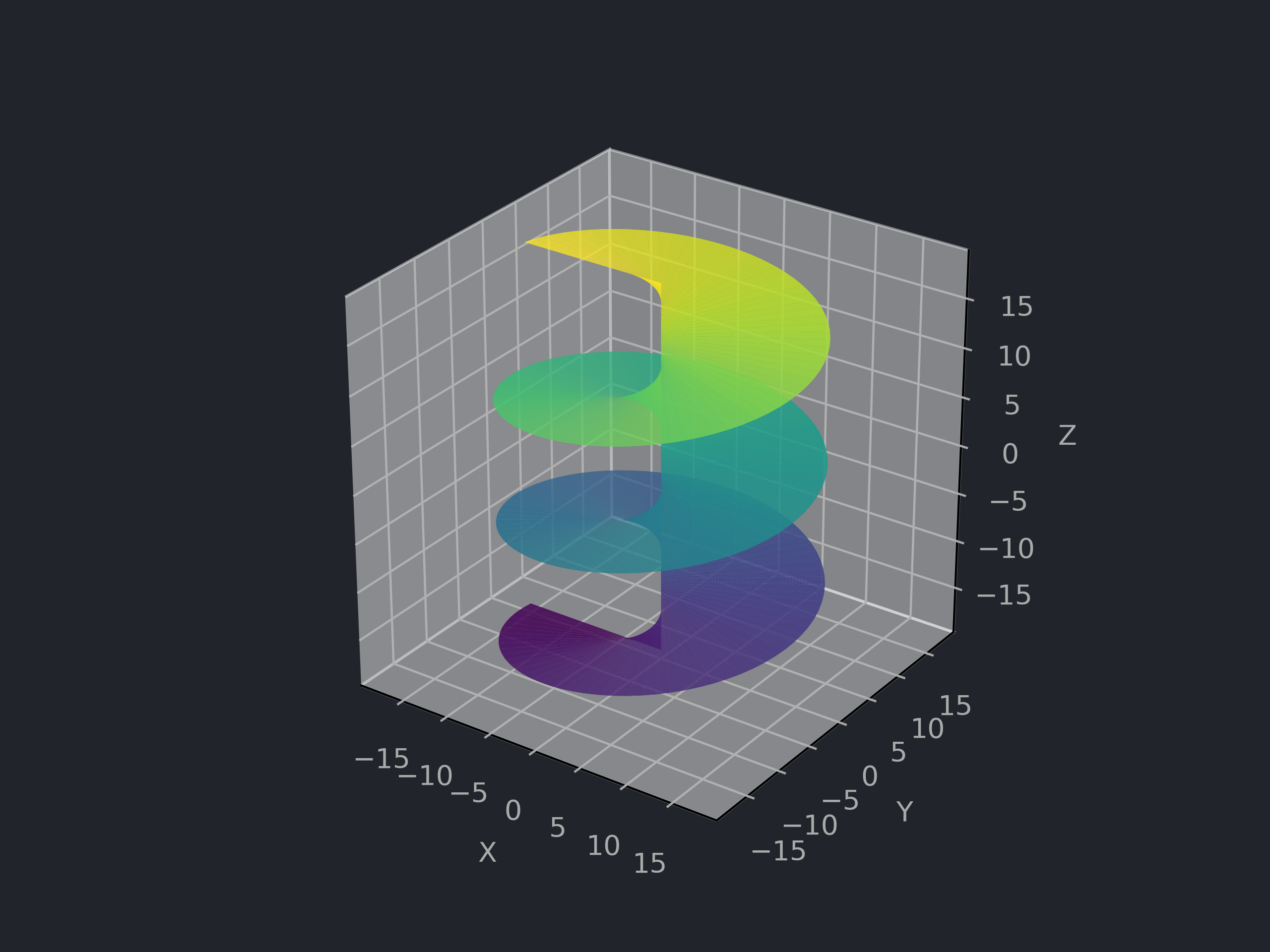
# 螺旋面 Helicoid

# 曲面方程与参数表示

$k > 0,\ D = \mathbb R^2$

$$f(x,y,z) = x \sin\frac{z}{k} - y \cos\frac{z}{k},\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} u \cos v \\ u \sin v \\ kv \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix}\cos v \\ \sin v \\ 0\end{pmatrix} \times \begin{pmatrix}0 \\ 0 \\ k\end{pmatrix} = \begin{pmatrix}k \sin v \\ -k \cos v \\ 0\end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \frac{1}{\sqrt{u^2 + k^2}} \begin{pmatrix} \sin v \\ -\cos v \\ \frac{u}{k} \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = 1$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = 0,$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = u^2 + k^2$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \boldsymbol 0,\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} -\sin v \\ \cos v \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} -u \cos v \\ -u \sin v \\ 0 \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = 0$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = -\frac{k}{\sqrt{u^2 + k^2}}$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = 0$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = -\frac{k^2}{(u^2 + k^2)^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = 0$$

$$\kappa_1 = \frac{k}{u^2 + k^2},\quad \kappa_2 = -\frac{k}{u^2 + k^2}$$

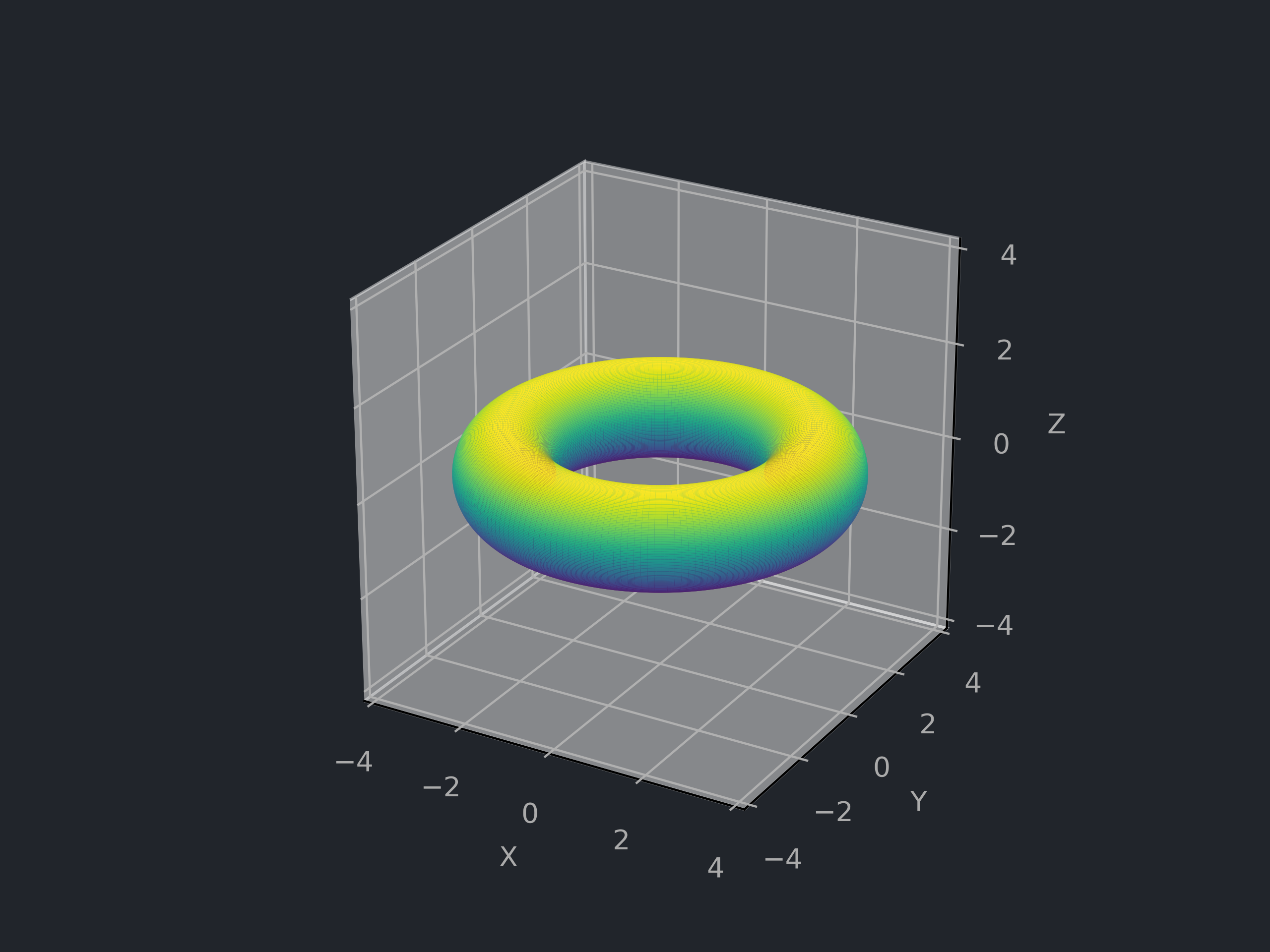
# 环面 Torus

# 曲面方程与参数表示

$R > r > 0,\quad D = (0,2\pi)^2$

$$f(x,y,z) = \left(\sqrt{x^2 + y^2} - R\right)^2 + z^2 - r^2,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} (R + r \cos u) \cos v \\ (R + r \cos u) \sin v \\ r \sin u \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} -r \sin u \cos v \\ -r \sin u \sin v \\ r \cos u \end{pmatrix} \times \begin{pmatrix} -(R + r \cos u) \sin v \\ (R + r \cos u) \cos v \\ 0 \end{pmatrix} = \begin{pmatrix} -r \cos u (R + r \cos u) \cos v \\ -r \cos u (R + r \cos u) \sin v \\ -r \sin u (R + r \cos u) \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \begin{pmatrix} -\cos u \cos v \\ -\cos u \sin v \\ -\sin u \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = r^2$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = 0,$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = (R + r \cos u)^2$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \begin{pmatrix} -r \cos u \cos v \\ -r \cos u \sin v \\ -r \sin u \end{pmatrix},\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} r \sin u \sin v \\ -r \sin u \cos v \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} -(R + r \cos u) \cos v \\ -(R + r \cos u) \sin v \\ 0 \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = r$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = (R + r \cos u) \cos u$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{\cos u}{r (R + r \cos u)}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{(R + 2r \cos u)}{2r (R + r \cos u)}$$

$$\kappa_1 = \frac{1}{r},\quad \kappa_2 = \frac{\cos u}{R + r \cos u}$$

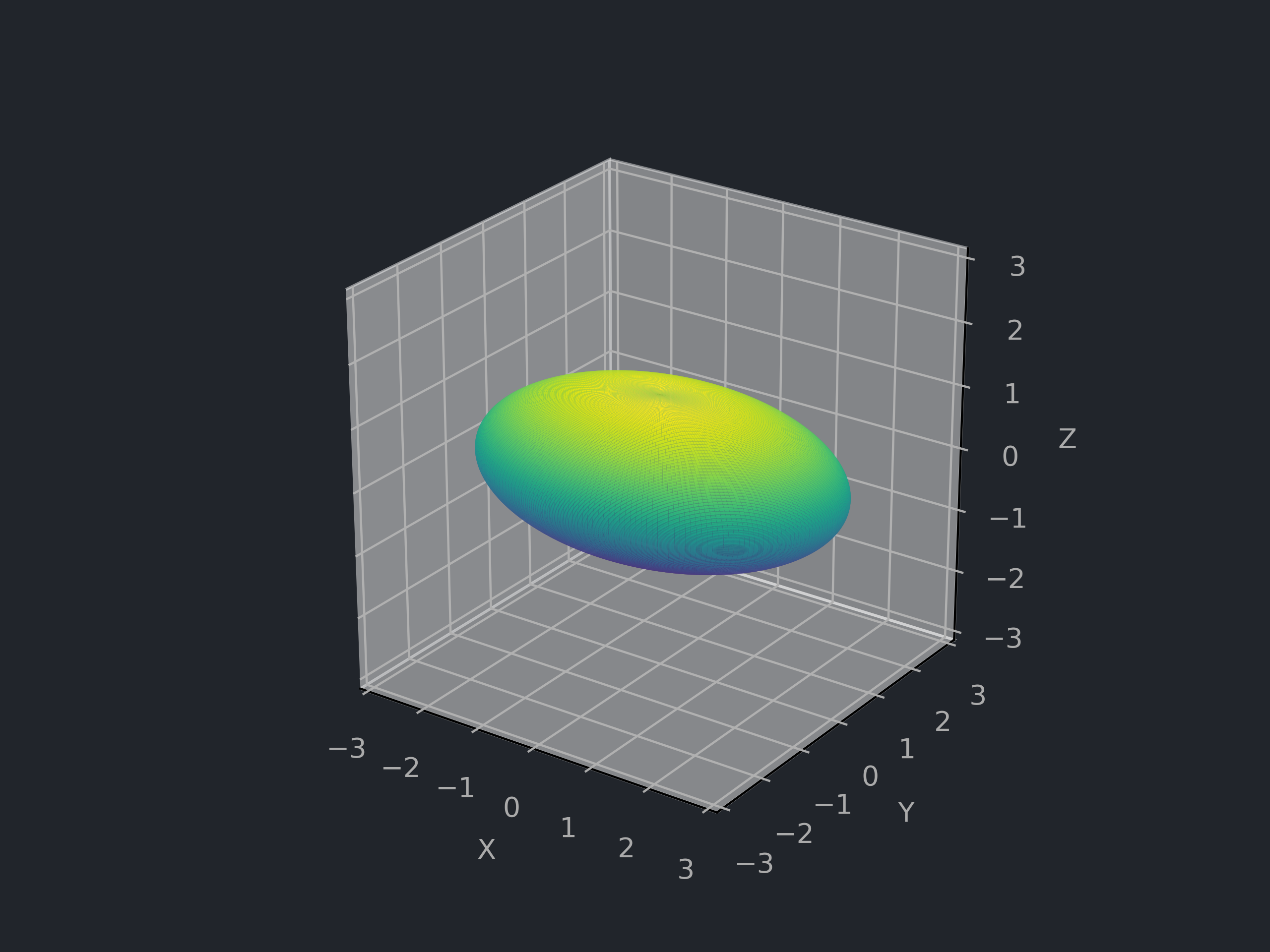
# 椭球 Ellipsoid

# 曲面方程与参数表示

$a,b,c > 0,\quad D = (0,\pi) \times (0,2\pi)$

$$f(x,y,z) = \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} - 1,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} a \sin u \cos v \\ b \sin u \sin v \\ c \cos u \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} a \cos u \cos v \\ b \cos u \sin v \\ -c \sin u \end{pmatrix} \times \begin{pmatrix} -a \sin u \sin v \\ b \sin u \cos v \\ 0 \end{pmatrix} = \begin{pmatrix} bc \sin^2 u \cos v \\ ac \sin^2 u \sin v \\ ab \sin u \cos u \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \frac{1}{\sqrt{c^2 \sin^2 u + ab \cos^2 u}} \begin{pmatrix} bc \sin u \cos v \\ ac \sin u \sin v \\ ab \cos u \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = a^2 \cos^2 u \cos^2 v + b^2 \cos^2 u \sin^2 v + c^2 \sin^2 u$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = 0,$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = a^2 \sin^2 u \sin^2 v + b^2 \sin^2 u \cos^2 v$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \begin{pmatrix} -a \sin u \cos v \\ -b \sin u \sin v \\ -c \cos u \end{pmatrix},\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} -a \cos u \sin v \\ b \cos u \cos v \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} -a \sin u \cos v \\ -b \sin u \sin v \\ 0 \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = \frac{abc \sin u}{\sqrt{c^2 \sin^2 u + ab \cos^2 u}}$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = \frac{ab \sin u}{\sqrt{c^2 \sin^2 u + ab \cos^2 u}}$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{abc}{(c^2 \sin^2 u + ab \cos^2 u)^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{abc (a^2 + b^2 + c^2 - 2(a^2 - c^2) \sin^2 u - 2(b^2 - c^2) \sin^2 u \cos^2 v)}{2 (c^2 \sin^2 u + ab \cos^2 u)^{3/2} (a^2 \sin^2 u \sin^2 v + b^2 \sin^2 u \cos^2 v + c^2 \cos^2 u)}$$

$$\kappa_1 = \frac{abc}{(c^2 \sin^2 u + ab \cos^2 u)^{3/2}},\quad \kappa_2 = \frac{abc}{\sqrt{c^2 \sin^2 u + ab \cos^2 u} (a^2 \sin^2 u \sin^2 v + b^2 \sin^2 u \cos^2 v + c^2 \cos^2 u)}$$

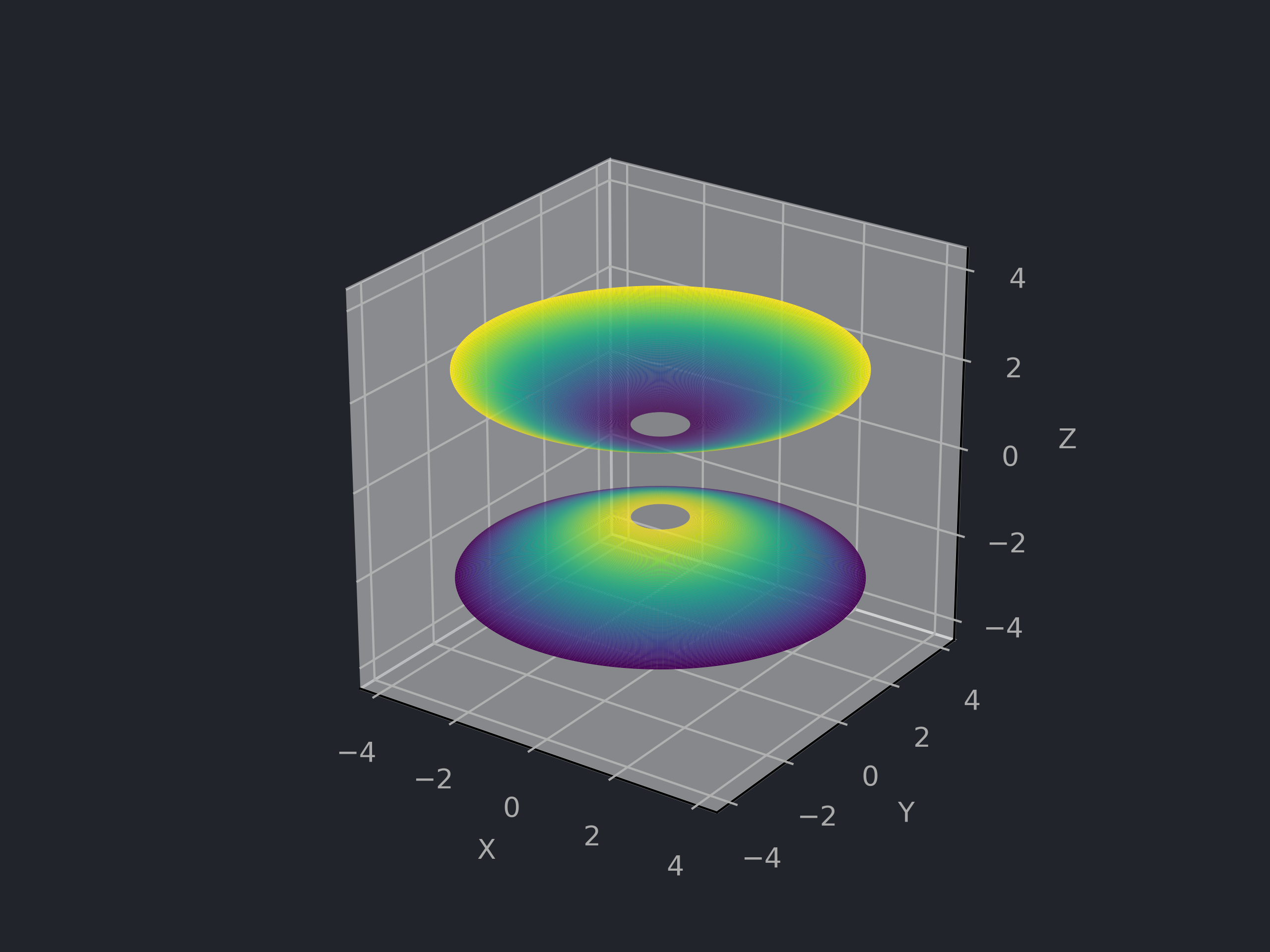
# 单叶双曲面 Hyperbolioid

# 曲面方程与参数表示

$a,b,c > 0,\quad D = \mathbb R \times (0,2\pi)$

$$f(x,y,z) = \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} - 1,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} a \cosh u \cos v \\ b \cosh u \sin v \\ c \sinh u \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} a \sinh u \cos v \\ b \sinh u \sin v \\ c \cosh u \end{pmatrix} \times \begin{pmatrix} -a \cosh u \sin v \\ b \cosh u \cos v \\ 0 \end{pmatrix} = \begin{pmatrix} -bc \cosh u \sinh u \cos v \\ -ac \cosh u \sinh u \sin v \\ ab \cosh^2 u \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \frac{1}{\sqrt{c^2 \sinh^2 u + ab \cosh^2 u}} \begin{pmatrix} -bc \sinh u \cos v \\ -ac \sinh u \sin v \\ ab \cosh u \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = a^2 \sinh^2 u \cos^2 v + b^2 \sinh^2 u \sin^2 v - c^2 \cosh^2 u$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = 0,$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = a^2 \cosh^2 u \sin^2 v + b^2 \cosh^2 u \cos^2 v$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \begin{pmatrix} a \cosh u \cos v \\ b \cosh u \sin v \\ c \sinh u \end{pmatrix},\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} -a \sinh u \sin v \\ b \sinh u \cos v \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} -a \cosh u \cos v \\ -b \cosh u \sin v \\ 0 \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = \frac{-abc \cosh u}{\sqrt{c^2 \sinh^2 u + ab \cosh^2 u}}$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = \frac{-ab \cosh u}{\sqrt{c^2 \sinh^2 u + ab \cosh^2 u}}$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{-abc}{(c^2 \sinh^2 u + ab \cosh^2 u)^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{-abc (a^2 + b^2 - c^2 + 2(c^2 - a^2) \sinh^2 u + 2(c^2 - b^2) \sinh^2 u \cos^2 v)}{2 (c^2 \sinh^2 u + ab \cosh^2 u)^{3/2} (a^2 \cosh^2 u \sin^2 v + b^2 \cosh^2 u \cos^2 v - c^2 \sinh^2 u)}$$

$$\kappa_1 = \frac{-abc}{(c^2 \sinh^2 u + ab \cosh^2 u)^{3/2}},\quad \kappa_2 = \frac{-abc}{\sqrt{c^2 \sinh^2 u + ab \cosh^2 u} (a^2 \cosh^2 u \sin^2 v + b^2 \cosh^2 u \cos^2 v - c^2 \sinh^2 u)}$$

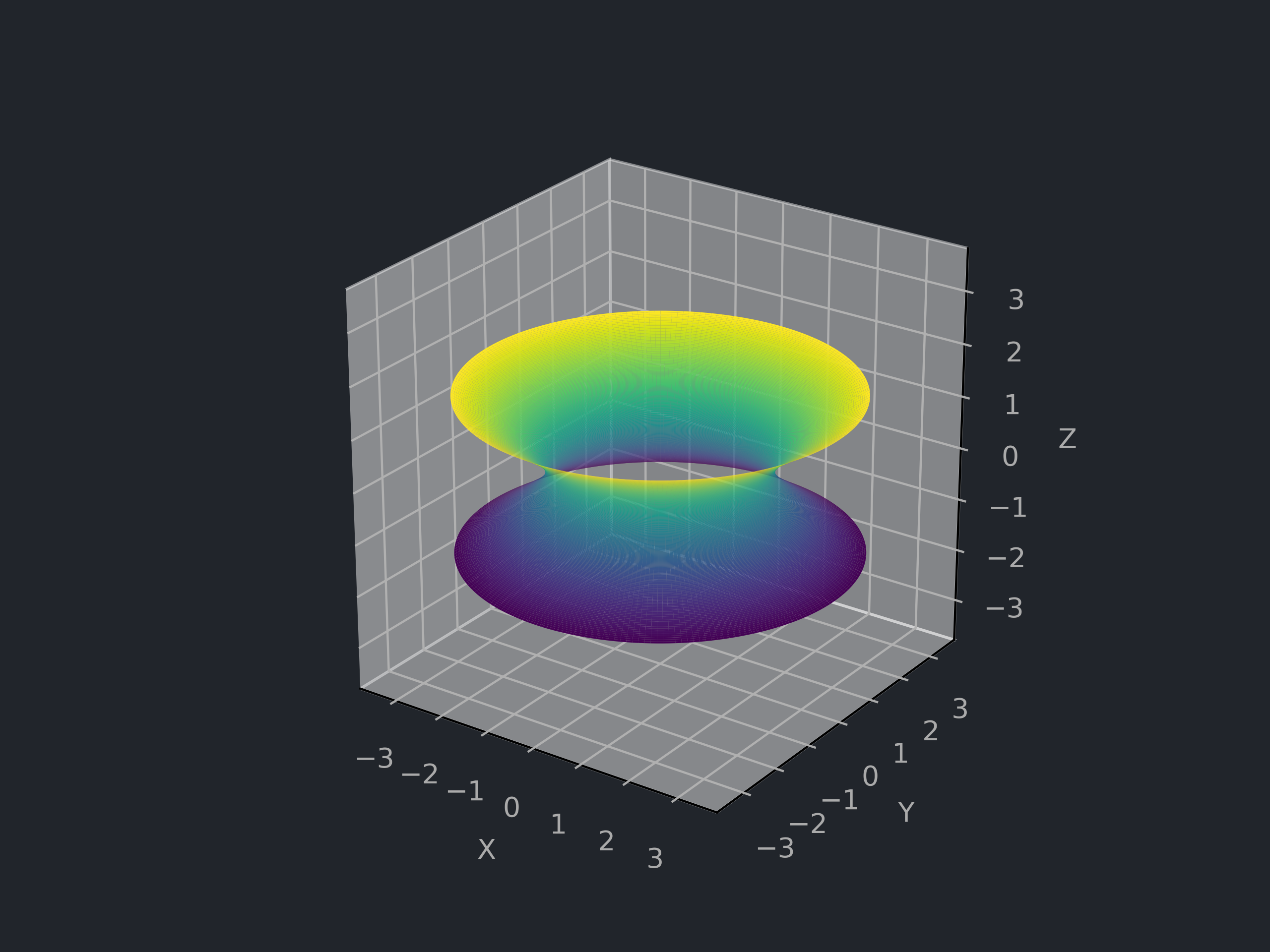
# 双叶双曲面 Hyperboloid of two sheets

# 曲面方程与参数表示

$a,b,c > 0,\quad D = \mathbb R \times (0,2\pi)$

$$f(x,y,z) = \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} + 1,\quad \boldsymbol \sigma_+(u,v) = \begin{pmatrix} au \\ bv \\ c \sqrt{\frac{x^2}{a^2} + \frac{y^2}{b^2} + 1} \end{pmatrix},\quad \boldsymbol \sigma_-(u,v) = \begin{pmatrix} au \\ bv \\ -c \sqrt{\frac{x^2}{a^2} + \frac{y^2}{b^2} + 1} \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_{+u} \times \boldsymbol \sigma_{+v} = \begin{pmatrix} a \\ 0 \\ \frac{cu}{\sqrt{u^2 + v^2 + 1}} \end{pmatrix} \times \begin{pmatrix} 0 \\ b \\ \frac{cv}{\sqrt{u^2 + v^2 + 1}} \end{pmatrix} = \begin{pmatrix} -\frac{bc v}{\sqrt{u^2 + v^2 + 1}} \\ -\frac{ac u}{\sqrt{u^2 + v^2 + 1}} \\ ab \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma_+(u,v)) = \frac{\boldsymbol \sigma_{+u} \times \boldsymbol \sigma_{+v}}{\|\boldsymbol \sigma_{+u} \times \boldsymbol \sigma_{+v}\|} = \frac{1}{\sqrt{c^2 (u^2 + v^2) + ab}} \begin{pmatrix} -bc v \\ -ac u \\ ab \end{pmatrix}$$

$$\boldsymbol \sigma_{-u} \times \boldsymbol \sigma_{-v} = \begin{pmatrix} a \\ 0 \\ -\frac{cu}{\sqrt{u^2 + v^2 + 1}} \end{pmatrix} \times \begin{pmatrix} 0 \\ b \\ -\frac{cv}{\sqrt{u^2 + v^2 + 1}} \end{pmatrix} = \begin{pmatrix} \frac{bc v}{\sqrt{u^2 + v^2 + 1}} \\ \frac{ac u}{\sqrt{u^2 + v^2 + 1}} \\ ab \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma_-(u,v)) = \frac{\boldsymbol \sigma_{-u} \times \boldsymbol \sigma_{-v}}{\|\boldsymbol \sigma_{-u} \times \boldsymbol \sigma_{-v}\|} = \frac{1}{\sqrt{c^2 (u^2 + v^2) + ab}} \begin{pmatrix} bc v \\ ac u \\ ab \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_{\pm u} \cdot \boldsymbol \sigma_{\pm u} = a^2 + \frac{c^2 u^2}{u^2 + v^2 + 1}$$

$$F = \boldsymbol \sigma_{\pm u} \cdot \boldsymbol \sigma_{\pm v} = \frac{c^2 uv}{u^2 + v^2 + 1},$$

$$G = \boldsymbol \sigma_{\pm v} \cdot \boldsymbol \sigma_{\pm v} = b^2 + \frac{c^2 v^2}{u^2 + v^2 + 1}$$

# 第二基本量

$$\boldsymbol \sigma_{\pm uu} = \begin{pmatrix} 0 \\ 0 \\ \pm \frac{c}{(u^2 + v^2 + 1)^{3/2}} \end{pmatrix},\quad \boldsymbol \sigma_{\pm uv} = \begin{pmatrix} 0 \\ 0 \\ \pm \frac{-c uv}{(u^2 + v^2 + 1)^{3/2}} \end{pmatrix},\quad \boldsymbol \sigma_{\pm vv} = \begin{pmatrix} 0 \\ 0 \\ \pm \frac{c}{(u^2 + v^2 + 1)^{3/2}} \end{pmatrix}$$

$$L = \boldsymbol \sigma_{\pm uu} \cdot \boldsymbol n = \frac{-abc}{(c^2 (u^2 + v^2) + ab) \sqrt{u^2 + v^2 + 1}}$$

$$M = \boldsymbol \sigma_{\pm uv} \cdot \boldsymbol n = \frac{abc uv}{(c^2 (u^2 + v^2) + ab) \sqrt{u^2 + v^2 + 1}}$$

$$N = \boldsymbol \sigma_{\pm vv} \cdot \boldsymbol n = \frac{-abc}{(c^2 (u^2 + v^2) + ab) \sqrt{u^2 + v^2 + 1}}$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{abc}{(c^2 (u^2 + v^2) + ab)^2 (u^2 + v^2 + 1)^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{-abc (a^2 + b^2 - c^2 + 2(c^2 + a^2) u^2 + 2(c^2 + b^2) v^2)}{2 (c^2 (u^2 + v^2) + ab)^{3/2} (u^2 + v^2 + 1)^{3/2} (a^2 + \frac{c^2 u^2}{u^2 + v^2 + 1} + b^2 + \frac{c^2 v^2}{u^2 + v^2 + 1})}$$

$$\kappa_1 = \frac{-abc}{(c^2 (u^2 + v^2) + ab)^{3/2} (u^2 + v^2 + 1)^{3/2}},\quad \kappa_2 = \frac{-abc}{\sqrt{c^2 (u^2 + v^2) + ab} (u^2 + v^2 + 1)^{1/2} (a^2 + \frac{c^2 u^2}{u^2 + v^2 + 1} + b^2 + \frac{c^2 v^2}{u^2 + v^2 + 1})}$$

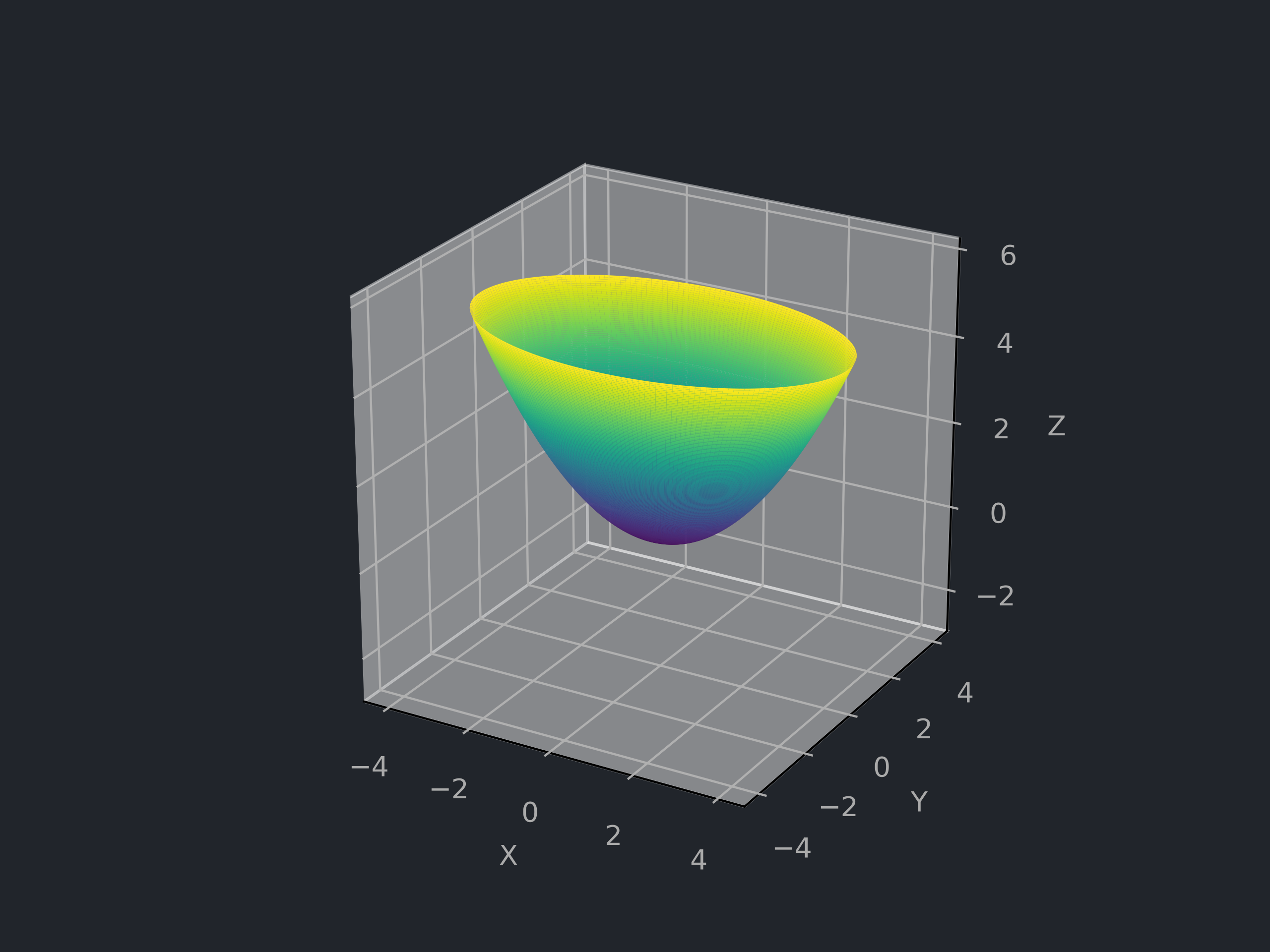
# 椭圆抛物面 Elliptic Paraboloid

# 曲面方程与参数表示

$a,b > 0,\quad D = \mathbb R^2$

$$f(x,y,z) = \frac{x^2}{a^2} + \frac{y^2}{b^2} - z = 0,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} u \\ v \\ \frac{u^2}{a^2} + \frac{v^2}{b^2} \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} 1 \\ 0 \\ \frac{2u}{a^2} \end{pmatrix} \times \begin{pmatrix} 0 \\ 1 \\ \frac{2v}{b^2} \end{pmatrix} = \begin{pmatrix} -\frac{2u}{a^2} \\ -\frac{2v}{b^2} \\ 1 \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \frac{1}{\sqrt{1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4}}} \begin{pmatrix} -\frac{2u}{a^2} \\ -\frac{2v}{b^2} \\ 1 \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = 1 + \frac{4u^2}{a^4}$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = \frac{4uv}{a^2 b^2},$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = 1 + \frac{4v^2}{b^4}$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \begin{pmatrix} 0 \\ 0 \\ \frac{2}{a^2} \end{pmatrix},\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} 0 \\ 0 \\ \frac{2}{b^2} \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = \frac{2/a^2}{\sqrt{1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4}}}$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = \frac{2/b^2}{\sqrt{1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4}}}$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{4}{a^2 b^2 (1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{(a^2 + b^2 + 4v^2) a^2 + (a^2 + b^2 + 4u^2) b^2}{a^2 b^2 (1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^{3/2}}$$

$$\kappa_1 = \frac{2/a^2}{(1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^{3/2}},\quad \kappa_2 = \frac{2/b^2}{(1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^{3/2}}$$

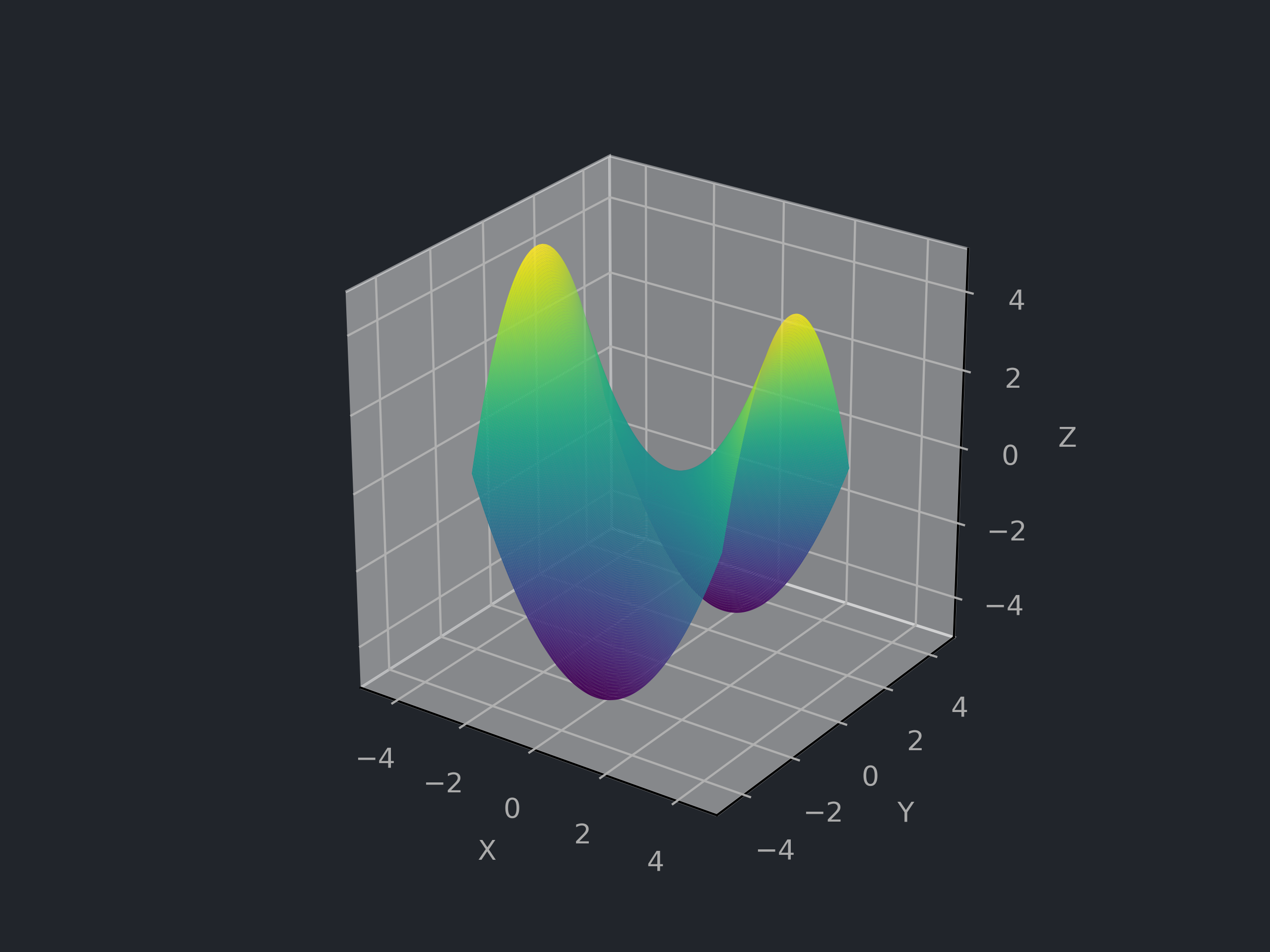
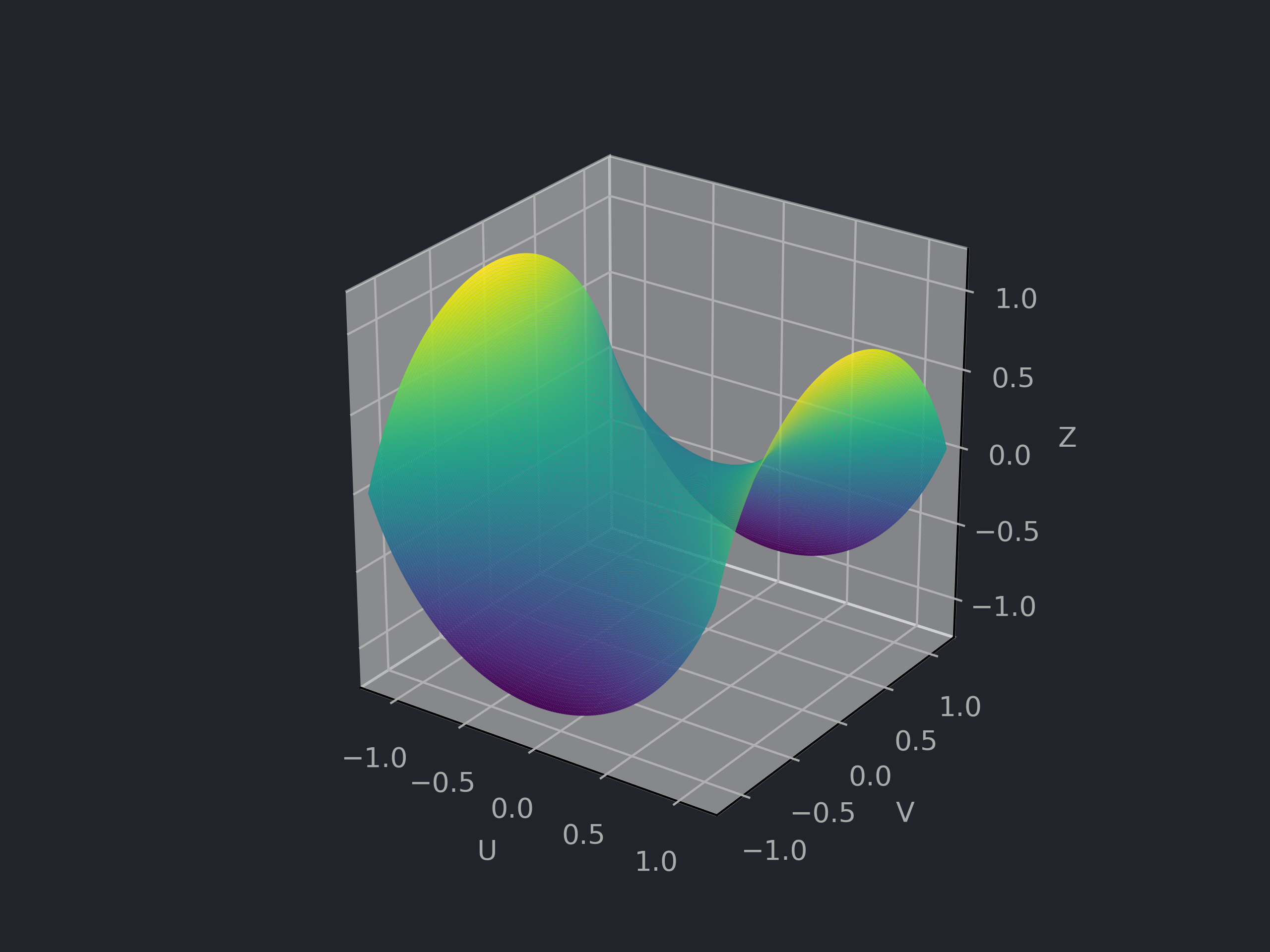
# 双曲抛物面 Hyperbolic Paraboloid

# 曲面方程与参数表示

$a,b > 0,\quad D = \mathbb R^2$

$$f(x,y,z) = \frac{x^2}{a^2} - \frac{y^2}{b^2} - z = 0,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} u \\ v \\ \frac{u^2}{a^2} - \frac{v^2}{b^2} \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} 1 \\ 0 \\ \frac{2u}{a^2} \end{pmatrix} \times \begin{pmatrix} 0 \\ 1 \\ -\frac{2v}{b^2} \end{pmatrix} = \begin{pmatrix} \frac{2u}{a^2} \\ -\frac{2v}{b^2} \\ 1 \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \frac{1}{\sqrt{1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4}}} \begin{pmatrix} \frac{2u}{a^2} \\ -\frac{2v}{b^2} \\ 1 \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = 1 + \frac{4u^2}{a^4}$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = -\frac{4uv}{a^2 b^2},$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = 1 + \frac{4v^2}{b^4}$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \begin{pmatrix} 0 \\ 0 \\ \frac{2}{a^2} \end{pmatrix},\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} 0 \\ 0 \\ -\frac{2}{b^2} \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = \frac{2/a^2}{\sqrt{1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4}}}$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = \frac{-2/b^2}{\sqrt{1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4}}}$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = \frac{-4}{a^2 b^2 (1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^2}$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{(a^2 - b^2 - 4v^2) a^2 + (b^2 - a^2 + 4u^2) b^2}{a^2 b^2 (1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^{3/2}}$$

$$\kappa_1 = \frac{2/a^2}{(1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^{3/2}},\quad \kappa_2 = \frac{-2/b^2}{(1 + \frac{4u^2}{a^4} + \frac{4v^2}{b^4})^{3/2}}$$

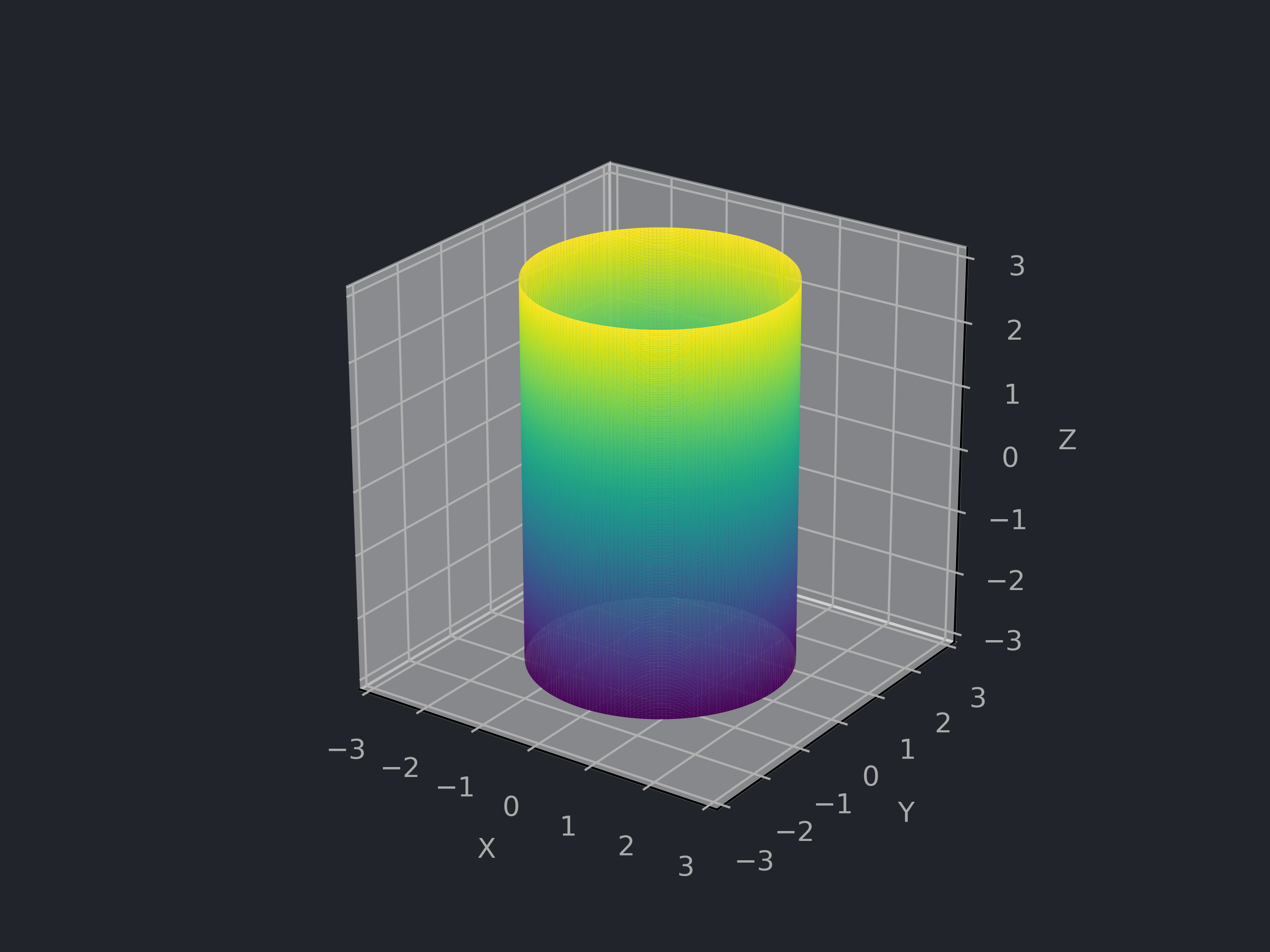
# 柱面 Cylinder

# 曲面方程与参数表示

$r > 0,\quad D = \mathbb R \times (0,2\pi)$

$$f(x,y,z) = x^2 + y^2 - r^2 = 0,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} r \cos v \\ r \sin v \\ u \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} -r \sin v \\ r \cos v \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} r \cos v \\ r \sin v \\ 0 \end{pmatrix}$$

$$\boldsymbol n(\boldsymbol \sigma(u,v)) = \frac{\boldsymbol \sigma_u \times \boldsymbol \sigma_v}{\|\boldsymbol \sigma_u \times \boldsymbol \sigma_v\|} = \frac{1}{\sqrt{r^2 \cos^2 v + r^2 \sin^2 v}} \begin{pmatrix} r \cos v \\ r \sin v \\ 0 \end{pmatrix} = \begin{pmatrix} \cos v \\ \sin v \\ 0 \end{pmatrix}$$

# 第一基本量

$$E = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_u = 1$$

$$F = \boldsymbol \sigma_u \cdot \boldsymbol \sigma_v = 0$$

$$G = \boldsymbol \sigma_v \cdot \boldsymbol \sigma_v = r^2$$

# 第二基本量

$$\boldsymbol \sigma_{uu} = \boldsymbol 0,\quad \boldsymbol \sigma_{uv} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\quad \boldsymbol \sigma_{vv} = \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix}$$

$$L = \boldsymbol \sigma_{uu} \cdot \boldsymbol n = 0$$

$$M = \boldsymbol \sigma_{uv} \cdot \boldsymbol n = 0$$

$$N = \boldsymbol \sigma_{vv} \cdot \boldsymbol n = \frac{2}{\sqrt{r^2 \cos^2 v + r^2 \sin^2 v}} = \frac{2}{r}$$

# 曲率

$$K = \frac{LN - M^2}{EG - F^2} = 0$$

$$H = \frac{EN - 2FM + GL}{2(EG - F^2)} = \frac{1}{2r}$$

$$\kappa_1 = 0,\quad \kappa_2 = \frac{1}{r}$$

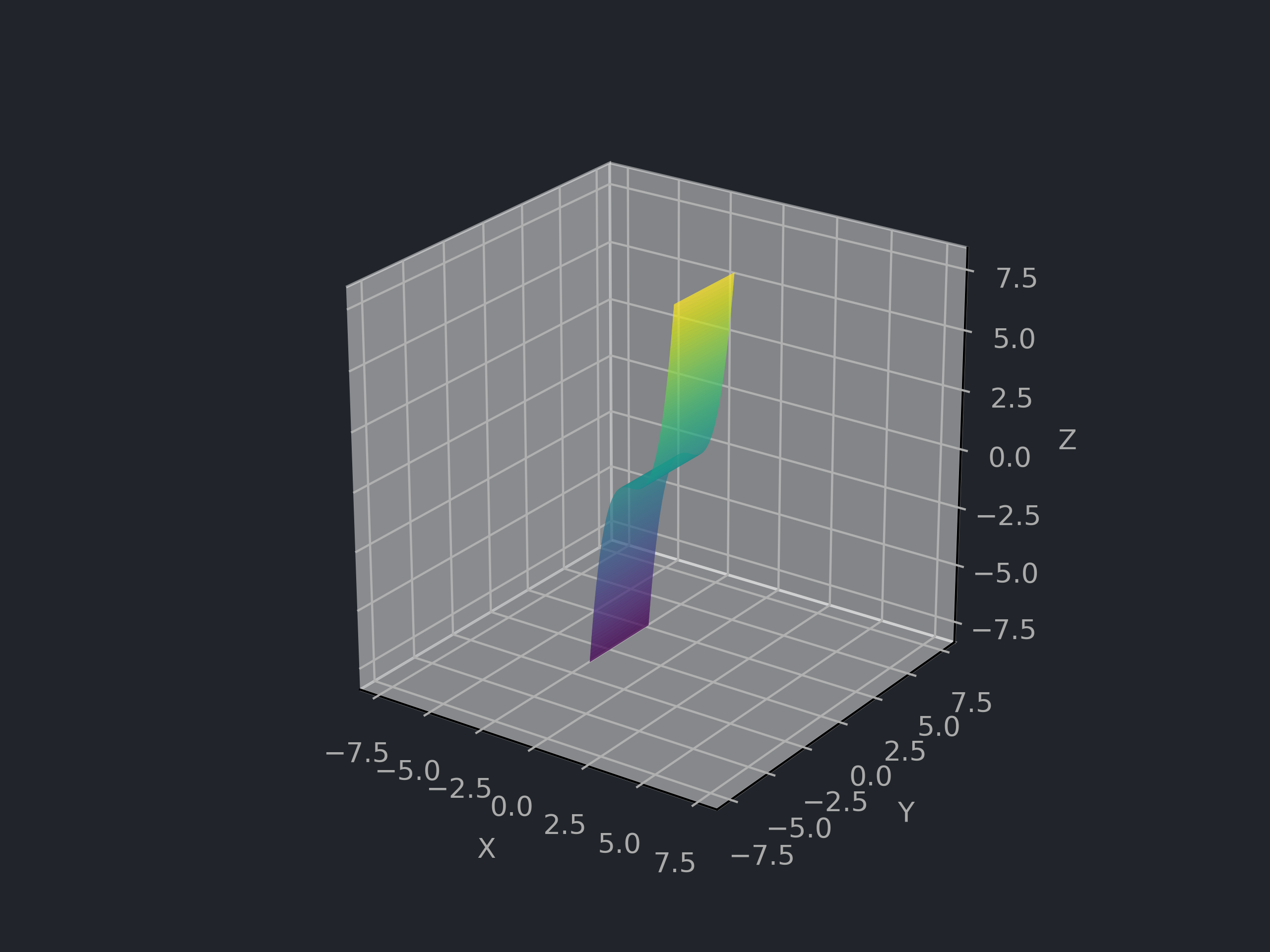
# 三次柱面 Cubic Cylinder

# 曲面方程与参数表示

$D = \mathbb R^2$

$$f(x,y,z) = y^2 - x^3 = 0,\quad \boldsymbol \sigma(u,v) = \begin{pmatrix} u \\ v \\ v^2 - u^3 \end{pmatrix}$$

# 正向法向量场

$$\boldsymbol \sigma_u \times \boldsymbol \sigma_v = \begin{pmatrix} 1 \\ 0 \\ -3u^2 \end{pmatrix} \times \begin{pmatrix} 0 \\ 1 \\ 2v \end{pmatrix} = \begin{pmatrix} 3u^2 \\ -2v \\ 1 \end{pmatrix}$$