# 变量代换

在引入积分问题之前，先思考如何改变曲面片的参数化的变量

称 $C^\infty$ 映射 $f: U(\subset \mathbb R^m) \to V(\subset \mathbb R^n)$ 为 微分同胚 (Diffeomorphism)「微分同相」，当且仅当 $f$ 是双射，并且 $f$ 与 $f^{-1}$ 都是光滑映射

命题
令 $E$ 为 $s-t$ 平面 $\mathbb R^2$ 中的非空开集， $D$ 为 $u-v$ 平面 $\mathbb R^2$ 中的非空开集， $\boldsymbol \sigma: D \to \mathbb R^3$ 为曲面片的参数化。
若 $\Phi: E \to D$ 是一个微分同胚，那么 $\boldsymbol \sigma \circ \Phi: E \to \mathbb R^3$ 也是一个曲面片的参数化，并且 $\boldsymbol \sigma(E) = (\boldsymbol \sigma \circ \Phi)(E)$

证明

设 $\boldsymbol \tau := \boldsymbol \sigma \circ \Phi$ ，作为复合映射，显然 $\boldsymbol \tau$ 是光滑且单射的
利用复合映射的偏微分，有

$\boldsymbol \tau_s(s,t) = \frac{\partial u}{\partial s} \boldsymbol \sigma_u + \frac{\partial v}{\partial s} \boldsymbol \sigma_v,\quad \boldsymbol \tau_t(s,t) = \frac{\partial u}{\partial t} \boldsymbol \sigma_u + \frac{\partial v}{\partial t} \boldsymbol \sigma_v$

计算向量积

$\begin{aligned} \boldsymbol \tau_s(s,t) \times \boldsymbol \tau_t(s,t) &= \left(\frac{\partial u}{\partial s} \boldsymbol \sigma_u + \frac{\partial v}{\partial s} \boldsymbol \sigma_v\right) \times \left(\frac{\partial u}{\partial t} \boldsymbol \sigma_u + \frac{\partial v}{\partial t} \boldsymbol \sigma_v\right) \\ &= \left( \frac{\partial u}{\partial s} \frac{\partial v}{\partial t} - \frac{\partial u}{\partial t} \frac{\partial v}{\partial s} \right) \boldsymbol \sigma_u \times \boldsymbol \sigma_v \\ &= J_\Phi(s,t) \cdot \boldsymbol \sigma_u \times \boldsymbol \sigma_v \end{aligned}$

由于 $\Phi$ 是微分同胚，所以 Jacobian 行列式 $J_\Phi(s,t) \neq 0$ ，又由于 $\boldsymbol \sigma$ 是曲面片的参数化，所以 $\boldsymbol \sigma_u \times \boldsymbol \sigma_v \neq \boldsymbol 0$ ，因此 $\boldsymbol \tau_s(s,t) \times \boldsymbol \tau_t(s,t) \neq \boldsymbol 0$ ， $\boldsymbol \tau$ 也是一个曲面片的参数化
$\square$

通过这样的方法，参数化 $\boldsymbol \sigma$ 变成了新的参数化 $\boldsymbol \sigma \circ \Phi$ ，称这样的操作为 变量代换 (Change of Variables)「変数変換」

称该代换是保持方向的，当且仅当 $J_\Phi(s,t) \gt 0$ $J_{Φ} (s, t) > 0$ 对任意 $(s,t) \in E$ $(s, t) \in E$ 都成立
- 此时 $\boldsymbol n_{\boldsymbol \sigma \circ \Phi}(s,t) = \boldsymbol n_{\boldsymbol \sigma}(u,v)$
称该代换是改变方向的，当且仅当 $J_\Phi(s,t) \lt 0$ $J_{Φ} (s, t) < 0$ 对任意 $(s,t) \in E$ $(s, t) \in E$ 都成立
- 此时 $\boldsymbol n_{\boldsymbol \sigma \circ \Phi}(s,t) = -\boldsymbol n_{\boldsymbol \sigma}(u,v)$

示例
一般地，由正则矩阵 $A$ 给出的线性映射

$\Phi: \mathbb R^2 \to \mathbb R^2,\quad \Phi(s,t) = A \begin{pmatrix}s \\ t\end{pmatrix}$

是一个微分同胚，且 $J_\Phi(s,t) = \det A$ 是常数

当 $\det A \gt 0$ 时， $\Phi$ 是保持方向的变量代换
当 $\det A \lt 0$ 时， $\Phi$ 是改变方向的变量代换

# 曲面积分

类似于在正则曲面之前引入了曲面片，曲面片作为曲面的基本单位，具备参数化的能力，这使得其法向量场可以由参数化的偏微分稳定给出

令 $S \subset \mathbb R^3$ 为以 $\boldsymbol \sigma: D \to \mathbb R^3$ 参数化的曲面片
我们来分析一下如何计算曲面片 $S$ 上的面积：
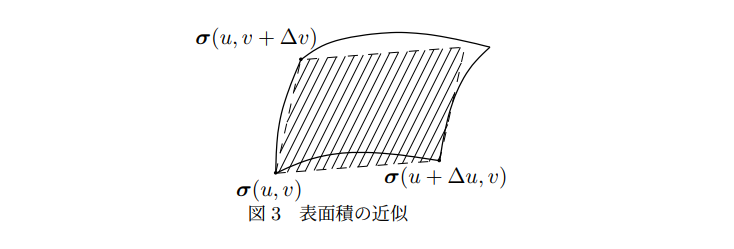
考虑位于点 $\boldsymbol \sigma(u,v)$ 处的一个小片段
曲面积近似示例

考虑偏微分向量积的模长

$\begin{aligned} \|\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)\| &= \left\| \lim_{\triangle u, \triangle v \to 0} \frac{\boldsymbol \sigma(u + \triangle u, v) - \boldsymbol \sigma(u,v)}{\triangle u} \times \frac{\boldsymbol \sigma(u, v + \triangle v) - \boldsymbol \sigma(u,v)}{\triangle v} \right\| \\ &= \lim_{\triangle u, \triangle v \to 0} \left\| \frac{\boldsymbol \sigma(u + \triangle u, v) - \boldsymbol \sigma(u,v)}{\triangle u} \times \frac{\boldsymbol \sigma(u, v + \triangle v) - \boldsymbol \sigma(u,v)}{\triangle v} \right\| \\ &= \lim_{\triangle u, \triangle v \to 0} \frac{\|(\boldsymbol \sigma(u + \triangle u, v) - \boldsymbol \sigma(u,v)) \times (\boldsymbol \sigma(u, v + \triangle v) - \boldsymbol \sigma(u,v))\|}{|\triangle u| \cdot |\triangle v|} \end{aligned}$

因此，当 $\triangle u$ 与 $\triangle v$ 足够小时，可以近似

也就是说，令矩形 $R := [u, u + \triangle u] \times [v, v + \triangle v]$ ，则 $\boldsymbol \sigma(R)$ 的面积近似为这里的曲面面积。
那么统合所有小矩形的面积近似，就可以得到曲面片 $S$ 的面积近似

定义
令 $S \subset \mathbb R^3$ 为以 $\boldsymbol \sigma: D \to \mathbb R^3$ 参数化的曲面片
设曲面的一部分 $T \subset S$ 的原象可测，那么其 曲面积 (Surface Area)「曲面積」 定义为

$\mathrm{Area}(T) = \iint_{\boldsymbol \sigma^{-1}(T)} \|\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)\| du dv$

从上述结果不难看出，曲面积分上的基本单位为 $dA = \|\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)\| du dv$ ，对于标量场的面积分，只需要给这个基本单位加上标量场的值。
但是对于向量场，类似向量场的曲线积分处理方式，需要将其与法向量场点积后再积分
一般地，曲面片上的积分按照如下给出

定义 曲面片的面积分
令 $S \subset \mathbb R^3$ 为以 $\boldsymbol \sigma: D \to \mathbb R^3$ 参数化的曲面片， $T \subset S$ 的原象可测

定义 $T$ 上连续标量场 $f: T \to \mathbb R$ 的面积分为

$\iint_T f dA = \iint_{\boldsymbol \sigma^{-1}(T)} f(\boldsymbol \sigma(u,v)) \|\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)\| du dv$

定义 $T$ 上连续向量场 $\boldsymbol F: T \to \mathbb R^3$ 的面积分为

$\iint_T \boldsymbol F d\boldsymbol A = \iint_{\boldsymbol \sigma^{-1}(T)} \boldsymbol F(\boldsymbol \sigma(u,v)) \cdot (\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)) du dv$

分别称

$dA = \|\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)\| du dv$ 为曲面片 $S$ 上的 面积元素 (Area Element)「面積要素」
$d\boldsymbol A = \boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v) du dv$ 为曲面片 $S$ 上的 向量面积元素 (Vector Area Element)「ベクトル面積要素」

接下来是正则曲面的面积分问题。由于正则曲面上的点不一定都可以被一个曲面片参数化，因此无法直接套用上述定义来计算面积分。
令 $S$ 为正则曲面。我们想要考虑某一个标量场或者向量场在 $T \subset S$ 上的面积分

如果 $T$ 是一个可以被正向参数化的曲面片，那么标量场和向量场的面积微元可以分别由下式给出

$dA = \|\boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v)\| du dv,\quad d\boldsymbol A = \boldsymbol \sigma_u(u,v) \times \boldsymbol \sigma_v(u,v) du dv$

但是通常来说无法默认 $T$ 是一个曲面片。因此可以类似于曲线积分中分段光滑的概念，考虑 $T$ 是否可以被多个曲面片分割。

定义 正则曲面的面积分
令 S 为 $\mathbb R^3$ 中的正则曲面， $T \subset S$ ，设存在一系列子集 $T_1, T_2, \cdots, T_n \subset S$ 满足

$T = \bigcup_{i=1}^n T_i$
每个 $T_i$ 都可以被一个曲面片参数化，即存在 $\boldsymbol \sigma_i: D_i \to \mathbb R^3$ 使得 $\boldsymbol \sigma_i(D_i) = T_i$ ，并且 $D_i$ 可测
$i \neq j$ 时， $T_i \cap T_j$ 的面积为零

那么，定义沿曲面 $T$ 的

标量场 $f: T \to \mathbb R$ 的面积分为

$\iint_T f dA = \sum_{i=1}^n \iint_{T_i} f dA$

向量场 $\boldsymbol F: T \to \mathbb R^3$ 的面积分为

$\iint_T \boldsymbol F d\boldsymbol A = \sum_{i=1}^n \iint_{T_i} \boldsymbol F d\boldsymbol A$

这样一来，正则曲面的面积分问题转为多个曲面片的面积分问题。用求和符号可以改写为

$\begin{aligned} \iint_T f dA &= \sum_{i=1}^n \iint_{D_i} f(\boldsymbol \sigma_i(u,v)) \|\boldsymbol \sigma_{i,u}(u,v) \times \boldsymbol \sigma_{i,v}(u,v)\| du dv \\ \iint_T \boldsymbol F d\boldsymbol A &= \sum_{i=1}^n \iint_{D_i} \boldsymbol F(\boldsymbol \sigma_i(u,v)) \cdot (\boldsymbol \sigma_{i,u}(u,v) \times \boldsymbol \sigma_{i,v}(u,v)) du dv \end{aligned}$

# Stokes 定理

Stokes 定理一定程度上可以说是 Green 定理的曲面推广

定理 Stokes 定理
令 $S$ 为以 $\boldsymbol \sigma: D \to \mathbb R^3$ 参数化的曲面片
领域 $\Omega \subset D$ 的边界 $\partial \Omega$ 是由分段光滑的正则单纯闭曲线 $C_0, C_1, \cdots, C_\ell$ 组成的，并且满足 $\overline \Omega \subset D$
那么经由 $\boldsymbol \sigma$ 的映射，各个像 $\boldsymbol \sigma(C_i)$ 也是分段光滑的正则单纯闭曲线，且在 $S$ 中包围了一个区域 $\boldsymbol \sigma(\overline \Omega)$
此时，对于定义在 $U \supset \boldsymbol \sigma(\overline \Omega)$ 上的连续向量场 $\boldsymbol F: U \to \mathbb R^3$ ，有

$\iint_{\boldsymbol \sigma(\overline \Omega)} \mathrm{curl} \boldsymbol F \cdot d\boldsymbol A = \sum_{i=0}^\ell \int_{\boldsymbol \sigma(C_i)} \boldsymbol F \cdot d\boldsymbol x$

证明

Stokes 定理的正式证明将在微分形式的章节给出，此处暂时省略

$\square$

作为一个特例，Stokes 在闭曲面上的结论广为人知

定义
称正则曲面 $S$ 是 封闭曲面 (Closed Surface)「閉曲面」，当且仅当 $S$ 是有界的，且是闭集

在开始给出闭曲面上的 Stokes 定理之前，让我们接触三角剖分

定义 三角形
令 $S$ 为正则曲面， $\boldsymbol \sigma:D \to \mathbb R^3$ 为 $S$ 的局部参数化
令 $\Omega \subset \mathbb R^2$ 满足 $\overline \Omega \subset D$ ，称像 $\boldsymbol \sigma(\Omega)$ 是 $S$ 上的一个 三角形 (Triangle)「三角形」，当且仅当 $\Omega$ 以三个正则曲线连接所得的单纯闭曲线作为边界的区域

# 变量代换

# 曲面积分

# Stokes 定理

【EJU】数学

备考笔记目录